Power function of a test
A function characterizing the quality of a statistical test. Suppose that, based on a realization  of a random vector
of a random vector  with values in a sampling space
with values in a sampling space  ,
,  , it is necessary to test the hypothesis
, it is necessary to test the hypothesis  according to which the probability distribution
according to which the probability distribution  of
of  belongs to a subset
belongs to a subset  , against the alternative
, against the alternative  according to which
according to which
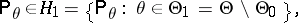 |
and let  be the critical function of the statistical test intended for testing
be the critical function of the statistical test intended for testing 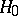 against
against 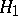 . Then
. Then
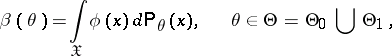 | (*) |
is called the power function of the statistical test with critical function  . It follows from (*) that
. It follows from (*) that  gives the probabilities with which the statistical test for testing
gives the probabilities with which the statistical test for testing  against
against  rejects the hypothesis
rejects the hypothesis 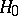 if
if  is subject to the law
is subject to the law 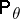 ,
, 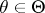 .
.
In the theory of statistical hypothesis testing, founded by J. Neyman and E. Pearson, the problem of testing a compound hypothesis 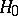 against a compound alternative
against a compound alternative  is formulated in terms of the power function of a test and consists of the construction of a test maximizing
is formulated in terms of the power function of a test and consists of the construction of a test maximizing  , when
, when 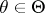 , under the condition that
, under the condition that  for all
for all  , where
, where  (
(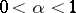 ) is called the significance level of the test — a given admissible probability of the error of rejecting
) is called the significance level of the test — a given admissible probability of the error of rejecting  when it is in fact true.
when it is in fact true.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959) |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [3] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
Power function of a test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_function_of_a_test&oldid=14564