Potentials, method of
A method for studying boundary value problems in mathematical physics by reducing them to integral equations; this method consists in representing the solutions of these problems in the form of (generalized) potentials.
Let a second-order elliptic partial differential equation be given in 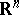 ,
, 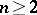 ,
,
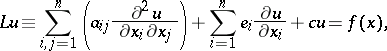 | (1) |
with sufficiently smooth coefficients 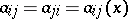 ,
, 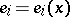 ,
, 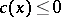 , and right-hand side
, and right-hand side 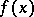 ; moreover, let
; moreover, let 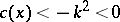 outside some bounded domain containing in its interior a domain
outside some bounded domain containing in its interior a domain 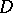 with boundary
with boundary 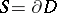 of class
of class 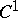 . Then any solution
. Then any solution 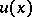 of class
of class 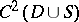 of (1) can be represented as the sum of three (generalized) potentials: a volume mass potential (cf. Newton potential)
of (1) can be represented as the sum of three (generalized) potentials: a volume mass potential (cf. Newton potential)
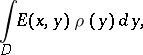 | (2) |
a single-layer potential (cf. Simple-layer potential)
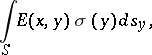 | (3) |
and a double-layer potential
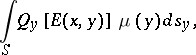 | (4) |
where 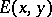 is a principal fundamental solution of
is a principal fundamental solution of 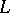 , the symbol
, the symbol 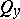 denotes the operator
denotes the operator
 |
acting at a point 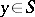 ,
,  is a unit co-normal vector at the point
is a unit co-normal vector at the point 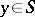 ,
,
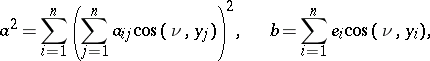 |
and  is the exterior normal vector to
is the exterior normal vector to 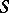 at
at 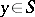 . The potential densities
. The potential densities 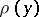 ,
, 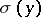 and
and 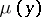 are sufficiently-smooth functions in
are sufficiently-smooth functions in 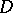 or on
or on 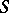 .
.
All differentiability and boundary properties of harmonic potentials described in the article Potential theory for the case when 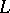 is the Laplace operator are valid for the potentials (2)–(4). On the basis of these properties one can reduce boundary value problems for elliptic equations of type (1) to integral equations in the same way as it has been done in the case of the Dirichlet and Neumann problems for harmonic functions in the article Potential theory.
is the Laplace operator are valid for the potentials (2)–(4). On the basis of these properties one can reduce boundary value problems for elliptic equations of type (1) to integral equations in the same way as it has been done in the case of the Dirichlet and Neumann problems for harmonic functions in the article Potential theory.
References
| [1] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [2] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
| [3] | V.S. Vladimirov, "Equations of mathematical physics" , M. Dekker (1971) (Translated from Russian) |
| [4] | V.D. Kupradze, "The method of potentials in elasticity theory" , Moscow (1963) (In Russian) |
| [5] | L.M. Milne-Thomson, "Theoretical hydrodynamics" , Macmillan (1949) |
Comments
References
| [a1] | J. Král, "Integral operators in potential theory" , Lect. notes in math. , 823 , Springer (1980) |
| [a2] | C.G. Simader, "On Dirichlet's boundary value problem" , Springer (1972) |
| [a3] | D.L. Colton, R. Kress, "Integral equation methods in scattering theory" , Wiley (1983) |
| [a4] | M. Jawson, G. Symm, "Integral equation methods in potential theory and elastostatics" , Acad. Press (1977) |
Potentials, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potentials,_method_of&oldid=17679