Difference between revisions of "Post canonical system"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48258 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''Post calculus'' | ''Post calculus'' | ||
| − | A way of defining enumerable sets (cf. [[Enumerable set|Enumerable set]]) of words. The notion of a Post canonical system was introduced in 1943 by E. Post and was the first general notion of a [[Calculus|calculus]] suitable to define arbitrary enumerable sets and not attached to the logical structure of the generated objects, to their semantics or to the logic of the derivation rules (cf. [[Derivation rule|Derivation rule]]). A Post canonical system is given by a quadruple | + | A way of defining enumerable sets (cf. [[Enumerable set|Enumerable set]]) of words. The notion of a Post canonical system was introduced in 1943 by E. Post and was the first general notion of a [[Calculus|calculus]] suitable to define arbitrary enumerable sets and not attached to the logical structure of the generated objects, to their semantics or to the logic of the derivation rules (cf. [[Derivation rule|Derivation rule]]). A Post canonical system is given by a quadruple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740001.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740002.png" /> is the alphabet of the calculus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740003.png" /> (which has no letters in common with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740004.png" />) is the alphabet of variables, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740005.png" /> is a list of words in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740006.png" /> (the axioms of the calculus), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740007.png" /> is a list of derivation rules of the form |
| − | where | ||
| − | is the alphabet of the calculus, | ||
| − | which has no letters in common with | ||
| − | is the alphabet of variables, | ||
| − | is a list of words in | ||
| − | the axioms of the calculus), and | ||
| − | is a list of derivation rules of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740008.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | ( | + | (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p0740009.png" /> are the designations of words in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400010.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400011.png" /> are the designations of letters from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400012.png" />). A word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400013.png" /> is obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400014.png" /> by applying the rule (*) if for any letter from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400015.png" /> in (*) one can find a word in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400016.png" /> (the value of this variable) after substitution of which at all places where the considered variable appears in (*) one obtains the words <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400017.png" /> above the line and the word <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400018.png" /> under the line. On the basis of such understanding of rules a derivation is defined in the Post canonical system. In the theory of calculi one uses the following definition of an enumerable set of words in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400019.png" />, which is equivalent to the usual one: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400020.png" /> is called enumerable if it coincides with a set of words in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400021.png" /> deduced in some Post canonical system whose alphabet contains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400022.png" /> (the necessity of the extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400023.png" /> by at least one letter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400024.png" /> is non-removable but one can require that besides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400025.png" /> only words of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400026.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400027.png" /> is in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400028.png" />, should be derivable). |
| − | are the designations of words in | ||
| − | |||
| − | are the designations of letters from | ||
| − | A word | ||
| − | is obtained from | ||
| − | by applying the rule (*) if for any letter from | ||
| − | in (*) one can find a word in | ||
| − | the value of this variable) after substitution of which at all places where the considered variable appears in (*) one obtains the words | ||
| − | above the line and the word | ||
| − | under the line. On the basis of such understanding of rules a derivation is defined in the Post canonical system. In the theory of calculi one uses the following definition of an enumerable set of words in | ||
| − | which is equivalent to the usual one: | ||
| − | is called enumerable if it coincides with a set of words in | ||
| − | deduced in some Post canonical system whose alphabet contains | ||
| − | the necessity of the extension of | ||
| − | by at least one letter | ||
| − | is non-removable but one can require that besides | ||
| − | only words of the form | ||
| − | where | ||
| − | is in | ||
| − | should be derivable). | ||
One can consider different specializations of the notion of a Post canonical system: 1) Post normal systems (all rules have the form | One can consider different specializations of the notion of a Post canonical system: 1) Post normal systems (all rules have the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400029.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
2) local calculi (rules of the form | 2) local calculi (rules of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400030.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
3) restricted calculi (a one-letter alphabet, rules with one premise); etc. | 3) restricted calculi (a one-letter alphabet, rules with one premise); etc. | ||
| Line 67: | Line 20: | ||
For references see [[Calculus|Calculus]]. | For references see [[Calculus|Calculus]]. | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | Regular canonical systems have turned out to be of particular importance. In a regular canonical system every derivation rule is of the form "Gp yields G'p" where | + | Regular canonical systems have turned out to be of particular importance. In a regular canonical system every derivation rule is of the form "Gp yields G'p" where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400032.png" /> are words over the alphabet of the calculus and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074000/p07400033.png" /> is a variable. Further details are contained in [[#References|[a1]]]. |
| − | and | ||
| − | are words over the alphabet of the calculus and | ||
| − | is a variable. Further details are contained in [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Salomaa, "Computation and automata" , Cambridge Univ. Press (1985)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Salomaa, "Computation and automata" , Cambridge Univ. Press (1985)</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
Post calculus
A way of defining enumerable sets (cf. Enumerable set) of words. The notion of a Post canonical system was introduced in 1943 by E. Post and was the first general notion of a calculus suitable to define arbitrary enumerable sets and not attached to the logical structure of the generated objects, to their semantics or to the logic of the derivation rules (cf. Derivation rule). A Post canonical system is given by a quadruple  , where
, where  is the alphabet of the calculus,
is the alphabet of the calculus,  (which has no letters in common with
(which has no letters in common with  ) is the alphabet of variables,
) is the alphabet of variables,  is a list of words in
is a list of words in  (the axioms of the calculus), and
(the axioms of the calculus), and  is a list of derivation rules of the form
is a list of derivation rules of the form
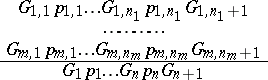 | (*) |
( are the designations of words in
are the designations of words in 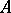 ;
; 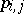 are the designations of letters from
are the designations of letters from  ). A word
). A word 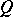 is obtained from
is obtained from 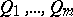 by applying the rule (*) if for any letter from
by applying the rule (*) if for any letter from 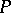 in (*) one can find a word in
in (*) one can find a word in  (the value of this variable) after substitution of which at all places where the considered variable appears in (*) one obtains the words
(the value of this variable) after substitution of which at all places where the considered variable appears in (*) one obtains the words 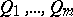 above the line and the word
above the line and the word 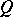 under the line. On the basis of such understanding of rules a derivation is defined in the Post canonical system. In the theory of calculi one uses the following definition of an enumerable set of words in
under the line. On the basis of such understanding of rules a derivation is defined in the Post canonical system. In the theory of calculi one uses the following definition of an enumerable set of words in  , which is equivalent to the usual one:
, which is equivalent to the usual one: 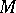 is called enumerable if it coincides with a set of words in
is called enumerable if it coincides with a set of words in  deduced in some Post canonical system whose alphabet contains
deduced in some Post canonical system whose alphabet contains 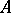 (the necessity of the extension of
(the necessity of the extension of  by at least one letter
by at least one letter  is non-removable but one can require that besides
is non-removable but one can require that besides  only words of the form
only words of the form 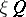 , where
, where 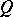 is in
is in 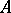 , should be derivable).
, should be derivable).
One can consider different specializations of the notion of a Post canonical system: 1) Post normal systems (all rules have the form
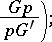 |
2) local calculi (rules of the form
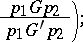 |
3) restricted calculi (a one-letter alphabet, rules with one premise); etc.
The above-mentioned specializations are assumed to have one axiom, and an arbitrary Post canonical system can be reduced to any of them (the equivalence between a Post canonical system and a Post normal calculus (cf. Post normal system) established by Post has fundamental significance in studies in this direction in order to find unsolvable systems).
For references see Calculus.
Comments
Regular canonical systems have turned out to be of particular importance. In a regular canonical system every derivation rule is of the form "Gp yields G'p" where  and
and 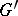 are words over the alphabet of the calculus and
are words over the alphabet of the calculus and  is a variable. Further details are contained in [a1].
is a variable. Further details are contained in [a1].
References
| [a1] | A. Salomaa, "Computation and automata" , Cambridge Univ. Press (1985) |
Post canonical system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Post_canonical_system&oldid=48258