Positive sequence
From Encyclopedia of Mathematics
A sequence  of real numbers in the interval
of real numbers in the interval  such that for any polynomial
such that for any polynomial
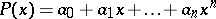 |
that is not identically zero and is not negative on  the expression
the expression
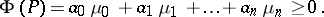 |
If for any such polynomial  , then the sequence is called strictly positive. For the sequence
, then the sequence is called strictly positive. For the sequence  in
in  to be positive, the existence of an increasing function
to be positive, the existence of an increasing function  on
on  for which
for which
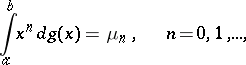 | (1) |
is necessary and sufficient.
Comments
A (strictly) negative sequence can be similarly defined and has a similar property. The problem of deciding whether for a given sequence  of real numbers there is a positive Borel measure
of real numbers there is a positive Borel measure 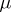 on
on  such that
such that 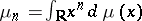 is known as the Hamburger moment problem. The condition (1) is a moment condition, cf. Moment problem.
is known as the Hamburger moment problem. The condition (1) is a moment condition, cf. Moment problem.
References
| [a1] | H.J. Landau (ed.) , Moments in mathematics , Amer. Math. Soc. (1987) pp. 56ff |
How to Cite This Entry:
Positive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_sequence&oldid=12427
Positive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_sequence&oldid=12427
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article