Positive-definite function on a group
From Encyclopedia of Mathematics
A continuous function  on the group
on the group  such that for all
such that for all  in
in  and
and  ,
,
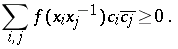 |
Examples can be obtained as follows. Let  be a unitary representation of
be a unitary representation of  in a Hilbert space
in a Hilbert space  , and let
, and let  be a unit (length) vector. Then
be a unit (length) vector. Then
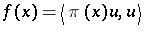 |
is a positive-definite function.
Essentially, these are the only examples. Indeed, there is a bijection between positive-definite functions on 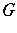 and isomorphism classes of triples
and isomorphism classes of triples 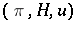 consisting of a unitary representation
consisting of a unitary representation 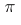 of
of 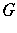 on
on 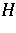 and a unit vector
and a unit vector 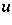 that topologically generates
that topologically generates 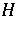 under
under 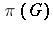 (a cyclic vector). This is the (generalized) Bochner–Herglotz theorem.
(a cyclic vector). This is the (generalized) Bochner–Herglotz theorem.
See also Fourier–Stieltjes transform (when 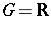 ).
).
References
| [a1] | S. Lang, "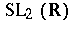 " , Addison-Wesley (1975) pp. Chap. IV, §5 " , Addison-Wesley (1975) pp. Chap. IV, §5 |
| [a2] | G.W. Mackey, "Unitary group representations in physics, probability and number theory" , Benjamin (1978) pp. 147ff |
How to Cite This Entry:
Positive-definite function on a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_function_on_a_group&oldid=18615
Positive-definite function on a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_function_on_a_group&oldid=18615
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article