Portion
From Encyclopedia of Mathematics
of a set
An intersection of the set with an interval in the case of a set on a line, and with an open ball, an open rectangle or an open parallelopipedon in the case of a set in an  -dimensional space
-dimensional space 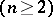 . The importance of this concept is based on the following. A set
. The importance of this concept is based on the following. A set 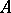 is everywhere dense in a set
is everywhere dense in a set 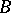 if every non-empty portion of
if every non-empty portion of 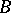 contains a point of
contains a point of 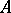 , in other words, if the closure
, in other words, if the closure 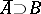 . The set
. The set 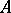 is nowhere dense in
is nowhere dense in 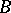 if
if 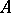 is nowhere dense in any portion of
is nowhere dense in any portion of 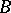 , i.e. if there does not exist a portion of
, i.e. if there does not exist a portion of 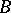 contained in
contained in 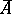 .
.
How to Cite This Entry:
Portion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Portion&oldid=16079
Portion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Portion&oldid=16079
This article was adapted from an original article by A.A. Konyushkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article