Pontryagin space
A Hilbert space with an indefinite metric 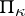 that has a finite rank of indefiniteness
that has a finite rank of indefiniteness 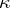 . Basic facts concerning the geometry of these spaces were established by L.S. Pontryagin [1]. Besides the facts common for spaces with an indefinite metric, the following properties hold.
. Basic facts concerning the geometry of these spaces were established by L.S. Pontryagin [1]. Besides the facts common for spaces with an indefinite metric, the following properties hold.
If 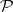 is an arbitrary non-negative linear manifold in
is an arbitrary non-negative linear manifold in 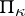 , then
, then 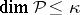 ; if
; if 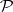 is a positive linear manifold and
is a positive linear manifold and 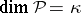 , then its
, then its 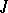 -orthogonal complement
-orthogonal complement 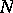 is a negative linear manifold and
is a negative linear manifold and 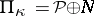 . Moreover,
. Moreover, 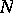 is a complete space with respect to the norm
is a complete space with respect to the norm 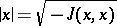 . If the linear manifold
. If the linear manifold 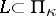 is non-degenerate, then its
is non-degenerate, then its 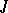 -orthogonal complement
-orthogonal complement  is non-degenerate as well and
is non-degenerate as well and 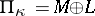 .
.
The spectrum (in particular, the discrete spectrum) of a 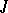 -unitary (
-unitary (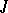 -self-adjoint) operator is symmetric with respect to the unit circle (real line), all elementary divisors corresponding to eigen values
-self-adjoint) operator is symmetric with respect to the unit circle (real line), all elementary divisors corresponding to eigen values 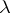 ,
, 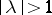 , are of finite order
, are of finite order 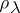 ,
, 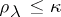 ,
, 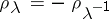 . The sum of the dimensions of the root subspaces of a
. The sum of the dimensions of the root subspaces of a 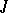 -unitary (
-unitary (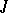 -self-adjoint) operator corresponding to eigen values
-self-adjoint) operator corresponding to eigen values 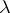 ,
, 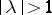 (
(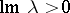 ), does not exceed
), does not exceed 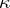 .
.
The following theorem [1] is fundamental in the theory of 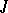 -self-adjoint operators on a Pontryagin space
-self-adjoint operators on a Pontryagin space 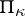 : For each
: For each 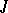 -self-adjoint operator
-self-adjoint operator 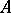 (
(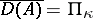 ) there exists a
) there exists a 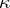 -dimensional (maximal) non-negative invariant subspace
-dimensional (maximal) non-negative invariant subspace 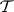 in which all eigen values of
in which all eigen values of 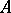 have non-negative imaginary parts, and a
have non-negative imaginary parts, and a 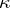 -dimensional non-negative invariant subspace
-dimensional non-negative invariant subspace 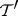 in which all eigen values have non-positive imaginary parts. A similar statement in which the upper (lower) half-plane is replaced by the exterior (interior) of the unit disc is also valid for
in which all eigen values have non-positive imaginary parts. A similar statement in which the upper (lower) half-plane is replaced by the exterior (interior) of the unit disc is also valid for 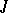 -unitary operators, and under certain additional conditions — even for operators on the space
-unitary operators, and under certain additional conditions — even for operators on the space 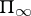 .
.
If 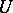 is a
is a 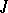 -unitary operator, then its maximal invariant subspaces
-unitary operator, then its maximal invariant subspaces 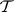 ,
, 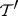 can be chosen so that the elementary divisors of the operator
can be chosen so that the elementary divisors of the operator 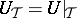 ,
, 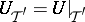 are of minimal order. In order that a polynomial
are of minimal order. In order that a polynomial 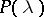 with no roots inside the unit disc has the property:
with no roots inside the unit disc has the property: 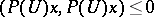 ,
, 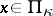 , it is necessary and sufficient that it can be divided by the minimal annihilating polynomial of the operator
, it is necessary and sufficient that it can be divided by the minimal annihilating polynomial of the operator 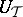 . If
. If 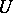 is a cyclic operator, then its non-negative invariant subspaces of dimension
is a cyclic operator, then its non-negative invariant subspaces of dimension 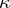 are uniquely determined. In this case the above-mentioned property of the polynomial
are uniquely determined. In this case the above-mentioned property of the polynomial 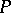 with roots
with roots 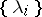 outside the unit disc,
outside the unit disc, 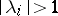 , is equivalent to the divisibility of
, is equivalent to the divisibility of 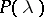 by the characteristic polynomial of
by the characteristic polynomial of 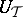 .
.
Each completely-continuous 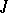 -self-adjoint operator
-self-adjoint operator 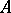 on a Pontryagin space
on a Pontryagin space 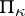 such that zero belongs to its continuous spectrum does not have a residual spectrum. The root vectors of such an operator form a Riesz basis in
such that zero belongs to its continuous spectrum does not have a residual spectrum. The root vectors of such an operator form a Riesz basis in 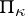 with respect to the (definite) norm
with respect to the (definite) norm 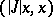 .
.
Many facts concerning invariant subspaces and the spectrum can be generalized to a case of 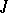 -isometric and
-isometric and 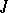 -non-expanding operators. Thus, if
-non-expanding operators. Thus, if 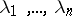 is an arbitrary set of eigen values of a
is an arbitrary set of eigen values of a 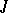 -isometric operator,
-isometric operator, 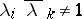 ,
, 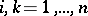 , and if
, and if 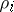 is the order of the elementary divisor at the point
is the order of the elementary divisor at the point 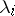 , then
, then 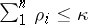 . Any
. Any 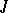 -non-expanding boundedly-invertible operator
-non-expanding boundedly-invertible operator 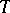 has a
has a 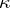 -dimensional invariant non-negative subspace
-dimensional invariant non-negative subspace 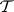 such that all eigen values of the restriction
such that all eigen values of the restriction 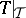 lie in the unit disc [2]. A similar fact holds for maximal
lie in the unit disc [2]. A similar fact holds for maximal 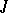 -dissipative operators. In general, a
-dissipative operators. In general, a 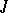 -dissipative operator
-dissipative operator 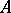 ,
, 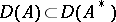 , has at most
, has at most 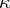 eigen values in the upper half-plane.
eigen values in the upper half-plane. 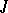 -isometric and
-isometric and 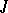 -symmetric (and more generally,
-symmetric (and more generally, 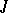 -non-expanding and
-non-expanding and 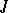 -dissipative) operators are related by the Cayley transformation (cf. Cayley transform), which has on
-dissipative) operators are related by the Cayley transformation (cf. Cayley transform), which has on 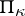 all natural properties [2]. This fact allows one to develop the extension theory simultaneously for
all natural properties [2]. This fact allows one to develop the extension theory simultaneously for 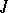 -isometric and
-isometric and 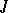 -symmetric operators. In particular, every
-symmetric operators. In particular, every 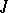 -isometric (
-isometric (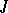 -symmetric) operator can be extended to a maximal one. If its deficiency indices are different, then it has no
-symmetric) operator can be extended to a maximal one. If its deficiency indices are different, then it has no 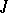 -unitary (
-unitary (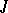 -self-adjoint) extensions. If these indices are equal and finite, then any maximal extension is
-self-adjoint) extensions. If these indices are equal and finite, then any maximal extension is 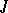 -unitary (
-unitary (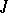 -self-adjoint).
-self-adjoint).
For completely-continuous operators on 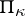 , a number of statements on the completeness of the system of root vectors, analogous to the corresponding facts from the theory of dissipative operators on spaces with a definite metric, is valid.
, a number of statements on the completeness of the system of root vectors, analogous to the corresponding facts from the theory of dissipative operators on spaces with a definite metric, is valid.
References
| [1] | L.S. Pontryagin, "Hermitian operators in a space with indefinite metric" Izv. Akad. Nauk. SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) |
| [2] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric I" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 105–175 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 |
| [3] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric II" Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 413–496 (In Russian) |
| [4] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with 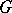 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 |
| [5] | M.G. Krein, "Introduction to the geometry of indefinite 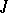 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [6] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" Itogi Nauk. i Tekhn. Mat. Anal. (1969) pp. 73–105 (In Russian) |
| [7] | L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
Comments
Pontryagin spaces form a subclass of the class of Krein spaces (cf. Krein space and also Hilbert space with an indefinite metric). The operator 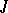 appearing in the beginning of the main article above is the fundamental symmetry (see Krein space), which defines the indefinite inner product via the formula
appearing in the beginning of the main article above is the fundamental symmetry (see Krein space), which defines the indefinite inner product via the formula 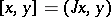 .
.
References
| [a1] | T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian) |
| [a2] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
Pontryagin space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_space&oldid=11492