Pompeiu problem
Let $X$ be a Hausdorff topological space (cf. also Hausdorff space; Topological space), $\mu$ a non-negative Radon measure on $X$, and $G$ a topological group of continuous self-mappings of $X$ leaving $\mu$ invariant. For $x \in X$ and $g \in G$, $g.x$ denotes the action of $g$ on $X$. A family $\mathcal{K}$ of compact subsets of $X$ is said to have the Pompeiu property if the linear mapping $P : C ( X ) \rightarrow \Pi _ { K \in \mathcal{K} } C ( G )$ given by
\begin{equation} \tag{a1} P f ( g ) = \left( \int _ { g K } f d \mu \right) _ { K \in \mathcal{K} } , g \in G, \end{equation}
is injective.
A typical example occurs when $X = \mathbf{R} ^ { n }$, $\mu$ is the Lebesgue measure, and $G = M ( n )$ is the Euclidean group of orientation-preserving rigid motions. Let $\chi _ { K }$ denote the characteristic function of $K$ and $\widehat { \chi }_{K}$ its Fourier transform, which is an entire function of exponential type (cf. also Entire function) in $\mathbf{C}^n$. In this case one can prove [a7], [a12] that $\mathcal{K}$ has the Pompeiu property if and only if
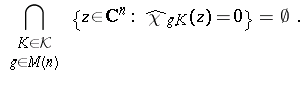 | (a2) |
When $\mathcal{K}$ is the ball, (a2) can never be satisfied but if $\mathcal{K} = \{ B _ { r _ { 1 } } , B _ { r _ { 2 } } \}$, a pair of balls of radii $r_1$ and $r_2$ (the centre plays no role in this case), then it has the Pompeiu property if and only if $r_{1} / r _ { 2 } \notin Z _ { n }$, where $Z_n$ is the set of fractions $\alpha / \beta$ for which $\alpha$ and $\beta$ are positive roots of $J _ { n / 2} ( r ) = 0$. (Here, $J _ { n / 2}$ is the Bessel function of the first kind and order $n / 2$, cf. Bessel functions.)
The key statement of the equivalence of the Pompeiu property with (a2) holds when $X$ is an irreducible symmetric space of rank $1$ and non-compact type and $G$ is its group of orientation-preserving isometries [a12].
When $\Omega$ is a bounded open set with Lipschitz boundary $\partial \Omega$ in ${\bf R} ^ { n }$ such that $\mathbf{R} ^ { n } \backslash \overline { \Omega }$ is connected, and if $G = M ( n )$, then failure of the Pompeiu property for the singleton $\mathcal{K} = \{ \overline { \Omega } \}$ is equivalent to the existence of an eigenvalue $\alpha > 0$ for the overdetermined Neumann boundary value problem for the Euclidean Laplacian (cf. also Neumann boundary conditions)
\begin{equation} \tag{a3} \left\{ \begin{array} { l } { \Delta u + \alpha u = 0 \quad \text { in } \Omega, } \\ { \frac { \partial u } { \partial n } = 0 \text { and } u = 1 \quad \text { on } \partial \Omega. } \end{array} \right. \end{equation}
It was shown by S. Williams [a9] that if (a3) has a solution, then $\partial \Omega$ must be real-analytic, which allows for many positive examples of the Pompeiu property. The equivalence between (a3) and the failure of Pompeiu property and Williams' observation also holds when $X$ is a non-compact symmetric space of rank $1$ with $\Delta$ the invariant Laplacian in this case [a4].
The natural conjecture that the existence of a solution $\alpha > 0$ for (a3) is equivalent to $\Omega$ being a Euclidean ball is usually called Schiffer's conjecture. For instance, [a1] contains the result that for convex planar sets the existence of infinitely many eigenvalues for (a3) implies that $\Omega$ is a disc. This inspired work of M. Agranovsky, C.A. Berenstein and P.C. Yang, N. Garofalo and F. Segala, T. Kobayashi, and others. See the excellent bibliographic survey [a11] for the details on the progress made on this conjecture up to date (1998), as well as general background on the Pompeiu property.
For $X = G = {\bf R} ^ { n }$ with $n \geq 2$, condition (a2) is only known to be necessary, due to the failure of the spectral synthesis, [a7]. For instance, for $n = 2$, except for elementary examples of the type of three squares with sides parallel to the axes and sizes $a$, $b$, $c$ none of whose quotients is rational, one can show that if one takes $K _ { 0 } \in \mathcal{K}$ to be, e.g., a rectangle, then (a2) is also sufficient for the Pompeiu property [a6].
This case of the Pompeiu problem has many applications in image and signal processing and leads to the problem of deconvolution, that is, given a finite family $K _ { 1 } , \dots , K _ { \text{l} }$, find distributions of compact support $\nu _ { 1 } , \dots , \nu _ { \text{l} }$ such that
\begin{equation*} \nu _ { 1 } * \chi _ { K _ { 1 } } + \ldots + \nu _ { 1 } { * } \chi _ { K _ { 1 } } = \delta, \end{equation*}
which amounts to finding a left inverse of the Pompeiu mapping (a1). See [a3], [a5], [a8] for details.
There is a local variant of the Pompeiu problem. For instance, let $X = B ( 0,1 )$ be the unit ball of ${\bf R} ^ { n }$, let $B _ { r _ { 1 } } , B _ { r _ { 2 } }$ be a pair of balls centred at the origin such that $r _ { 1 } + r _ { 2 } < 1$ and $r_1 / r _ { 2 } \notin \mathbf{Z} _ { n }$, then the values of all the integrals
\begin{equation*} \int _ { | x - a _ { j } | \leq r _ { j } } f ( x ) d x , \quad | a _ { j } | + r _ { j } < 1 ,\; j = 1,2, \end{equation*}
are enough to determine any function $f \in C ( X )$ (the Berenstein–Gay theorem); see [a2], [a10], [a11], for additional references, extensions, as well as relations to the deconvolution problem mentioned earlier.
References
| [a1] | C. Berenstein, "On the converse to Pompeiu's problem" Noteas e Communicaçoes de Mat. Univ. Fed. Pernambuco (Brazil) , 73 (1976) |
| [a2] | C. Berenstein, "The Pompeiu problem, What's new" R. Deville (ed.) et al. (ed.) , Complex Analysis, Harmonic Analysis and Applications , Res. Notes Math. , 347 , Pitman (1996) pp. 1–11 |
| [a3] | C. Berenstein, E.V. Patrick, "Exact deconvolution for multiple operators" IEEE Proc. Multidimensional Signal Proc. , 78 (1990) pp. 723–734 |
| [a4] | C. Berenstein, M. Shahshahani, "Harmonic analysis and the Pompeiu problem" Amer. J. Math. , 105 (1983) pp. 1217–1229 |
| [a5] | C. Berenstein, D. Struppa, "Complex analysis and convolution equations" G.M. Henkin (ed.) , Encycl. Math. Sci. , 54 (1993) pp. 1–108 |
| [a6] | C. Berenstein, B.A. Taylor, "The three-squares theorem for continuous functions" Arch. Rat. Mech. Anal. , 63 (1977) pp. 253–259 |
| [a7] | L. Brown, B. Schreiber, B.A. Taylor, "Spectral synthesis and the Pompeiu problem" Ann. Inst. Fourier , 23 : 3 (1973) pp. 125–154 |
| [a8] | S. Casey, D. Walnut, "Systems of convolution equations, deconvolution, Shannon sampling, and the wavelet and Gabor transforms" SIAM Review , 36 (1994) pp. 537–577 |
| [a9] | S. Williams, "A partial solution to the Pompeiu problem" Math. Ann. , 223 (1976) pp. 183–190 |
| [a10] | L. Zalcman, "Offbeat integral geometry" Amer. Math. Monthly , 87 (1980) pp. 161–175 |
| [a11] | L. Zalcman, "A bibliographic survey of the Pompeiu problem" B. Fuglede (ed.) et al. (ed.) , Approximation by solutions of partial differential equations , Kluwer Acad. Publ. (1992) pp. 185–194 (Addendum available from the author) |
| [a12] | C.A. Berenstein, L. Zalcman, "The Pompeiu problem in symmetric spaces" Comment. Math. Helvetici , 55 (1980) pp. 593–621 |
Pompeiu problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pompeiu_problem&oldid=14506