Polyhedron group
The group  of symmetries of a polytope (cf. Polyhedron)
of symmetries of a polytope (cf. Polyhedron)  in an
in an  -dimensional Euclidean space
-dimensional Euclidean space  , that is, the group of all motions of
, that is, the group of all motions of  which send
which send  to itself. A polytope
to itself. A polytope  is called regular if
is called regular if  acts transitively on the set of its "flag set of a polytopeflags" , that is, collections
acts transitively on the set of its "flag set of a polytopeflags" , that is, collections
 |
where 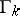 is a
is a  -dimensional closed face and
-dimensional closed face and 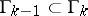 . The group of symmetries of a regular polytope is generated by reflections (see Reflection group). Its fundamental domain is a simplicial cone
. The group of symmetries of a regular polytope is generated by reflections (see Reflection group). Its fundamental domain is a simplicial cone  whose vertex is the centre of the polytope
whose vertex is the centre of the polytope  , and whose edges pass through the centres of the faces constituting some flag
, and whose edges pass through the centres of the faces constituting some flag  . By the same token the generating reflections
. By the same token the generating reflections  of the group
of the group  have a natural enumeration:
have a natural enumeration: 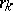 is the reflection relative to the hyperplane bounding
is the reflection relative to the hyperplane bounding  which does not pass through the centre of the face
which does not pass through the centre of the face  . The generators
. The generators  and
and 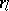 commute for
commute for 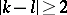 , and the order of
, and the order of  is equal to
is equal to 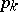 — the number of
— the number of 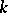 -dimensional (or
-dimensional (or  -dimensional) faces of the polytope
-dimensional) faces of the polytope 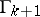 containing the face
containing the face 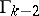 (if it is assumed that
(if it is assumed that 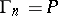 and
and  ). The sequence
). The sequence 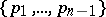 is called the Schläfli symbol of the polytopes. The three-dimensional regular polytopes (Platonic solids) have the following Schläfli symbols: the tetrahedron —
is called the Schläfli symbol of the polytopes. The three-dimensional regular polytopes (Platonic solids) have the following Schläfli symbols: the tetrahedron —  , the cube —
, the cube — 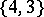 , the octahedron —
, the octahedron —  , the dodecahedron —
, the dodecahedron — 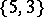 , and the icosahedron —
, and the icosahedron —  .
.
The Schläfli symbol determines a regular polytope up to a similarity. Reversal of a Schläfli symbol corresponds to transition to the reciprocal polytope, whose vertices ly at the centres of the 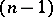 -dimensional faces of
-dimensional faces of  . Reciprocal polytopes have the same symmetry group.
. Reciprocal polytopes have the same symmetry group.
All possible Schläfli symbols of regular polytopes can be obtained from the classification of finite reflection groups, by selecting those with a linear Coxeter graph. For 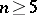 there are only 3 regular polytopes in
there are only 3 regular polytopes in  : the simplex, the cube and the polytope reciprocal to the cube (the analogue of the octahedron). Their Schläfli symbols are
: the simplex, the cube and the polytope reciprocal to the cube (the analogue of the octahedron). Their Schläfli symbols are  ,
,  and
and 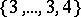 . In
. In 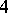 -dimensional space there are 6 regular polytopes:
-dimensional space there are 6 regular polytopes:  ,
,  ,
, 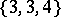 ,
, 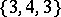 ,
, 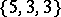 , and
, and  .
.
Each face of a regular polytope  is also a regular polytope, the Schläfli symbol of which is the initial segment of the Schläfli symbol of
is also a regular polytope, the Schläfli symbol of which is the initial segment of the Schläfli symbol of  . For example, a
. For example, a  -dimensional face of the polytope
-dimensional face of the polytope 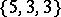 has the Schläfli symbol
has the Schläfli symbol  , that is, it is a dodecahedron.
, that is, it is a dodecahedron.
References
| [1] | H.S.M. Coxeter, "Regular polytopes" , Dover, reprint (1973) |
| [2] | B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian) |
Comments
A presentation of the polyhedron group is given by
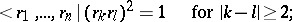 |
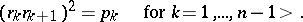 |
This shows that this group is a Coxeter group.
References
| [a1] | H.S.M. Coxeter, "Regular complex polytopes" , Cambridge Univ. Press (1990) |
Polyhedron group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polyhedron_group&oldid=12575