Polyhedron, abstract
The union of a locally finite family of convex polytopes in a certain  . By a convex polytope one understands the intersection of a finite number of closed half-spaces if this intersection is bounded. Local finiteness of the family means that each point in
. By a convex polytope one understands the intersection of a finite number of closed half-spaces if this intersection is bounded. Local finiteness of the family means that each point in  has a neighbourhood that intersects only with a finite number of the polytopes. A compact polyhedron is the union of a finite number of convex polytopes. The dimension of a polyhedron is the maximum dimension of the constituent polytopes. Any open subset of an (abstract) polyhedron, in particular any open subset of a Euclidean space, is a polyhedron. Other polyhedra are: the cone and the suspension over a compact polyhedron. Simple examples (a cone over an open interval) show that the join of a compact and a non-compact polyhedron need be not a polyhedron. The name subpolyhedron of a polyhedron
has a neighbourhood that intersects only with a finite number of the polytopes. A compact polyhedron is the union of a finite number of convex polytopes. The dimension of a polyhedron is the maximum dimension of the constituent polytopes. Any open subset of an (abstract) polyhedron, in particular any open subset of a Euclidean space, is a polyhedron. Other polyhedra are: the cone and the suspension over a compact polyhedron. Simple examples (a cone over an open interval) show that the join of a compact and a non-compact polyhedron need be not a polyhedron. The name subpolyhedron of a polyhedron  is given to any polyhedron
is given to any polyhedron  lying in
lying in  . Sometimes one restricts the consideration to closed subpolyhedra. Each point
. Sometimes one restricts the consideration to closed subpolyhedra. Each point  in a polyhedron
in a polyhedron  has in
has in  a neighbourhood that is a cone in
a neighbourhood that is a cone in  with vertex
with vertex  and with a compact base. This property is characteristic: Any subset in
and with a compact base. This property is characteristic: Any subset in  each point of which has a conical neighbourhood with a compact base is a polyhedron.
each point of which has a conical neighbourhood with a compact base is a polyhedron.
Any compact polyhedron  can be split up into a finite number of closed simplices in such a way that any two simplices either do not intersect or else intersect in a common face. In the case of a non-compact polyhedron it is required that the family of simplices should be locally finite. This decomposition is called a rectilinear triangulation of the polyhedron. Any two triangulations of a given polyhedron have a common subdivision. If
can be split up into a finite number of closed simplices in such a way that any two simplices either do not intersect or else intersect in a common face. In the case of a non-compact polyhedron it is required that the family of simplices should be locally finite. This decomposition is called a rectilinear triangulation of the polyhedron. Any two triangulations of a given polyhedron have a common subdivision. If 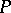 is a closed subpolyhedron of a polyhedron
is a closed subpolyhedron of a polyhedron 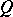 , then any triangulation
, then any triangulation  of
of 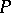 can be extended to a certain triangulation
can be extended to a certain triangulation  of
of  . In that case it is said that the resulting pair
. In that case it is said that the resulting pair  of geometrical simplicial complexes triangulates the pair
of geometrical simplicial complexes triangulates the pair 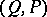 . A mapping
. A mapping  of a polyhedron
of a polyhedron  into a polyhedron
into a polyhedron 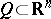 is called a piecewise-linear mapping (or a pl-mapping) if
is called a piecewise-linear mapping (or a pl-mapping) if 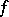 is simplicial with respect to certain triangulations of
is simplicial with respect to certain triangulations of 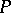 and
and 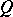 (cf. Simplicial mapping). An equivalent definition is that
(cf. Simplicial mapping). An equivalent definition is that  is piecewise linear if
is piecewise linear if 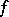 is locally conical, i.e. if each point
is locally conical, i.e. if each point  has a conical neighbourhood
has a conical neighbourhood  such that
such that 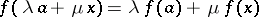 for any
for any  and
and  ,
, 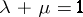 . For a mapping
. For a mapping  to be piecewise linear it is necessary and sufficient that its graph
to be piecewise linear it is necessary and sufficient that its graph 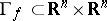 is a polyhedron.
is a polyhedron.
A superposition of piecewise-linear mappings is piecewise linear. The inverse mapping of an invertible piecewise-linear mapping 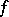 is piecewise linear. In that case
is piecewise linear. In that case  is called a pl-homeomorphism.
is called a pl-homeomorphism.
The category whose objects are polyhedra (and polyhedral pairs) and whose morphisms are pl-mappings is denoted by PL or by 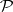 (see also Piecewise-linear topology). The category PL is one of the basic objects and tools of research in topology. The role of the category PL is particularly great in algebraic topology and in the topology of manifolds, because the class of polyhedra is fairly wide.
(see also Piecewise-linear topology). The category PL is one of the basic objects and tools of research in topology. The role of the category PL is particularly great in algebraic topology and in the topology of manifolds, because the class of polyhedra is fairly wide.
For example, each differentiable manifold can be represented in a natural way as a polyhedron. Each continuous mapping of one polyhedron into another can be approximated arbitrary closely by a pl-mapping. Therefore the category PL is a good approximation to the category of all topological spaces and continuous mappings. On the other hand, the triangulation of a polyhedron enables one to use methods from combinatorial topology. Many algebraic invariants (for example, the homology group or cohomology ring) can be constructed and effectively calculated by decomposition into simplices. The question whether all homeomorphic polyhedra are pl-homeomorphic is called the Hauptvermutung and the answer is negative: For  there exist homeomorphic
there exist homeomorphic  -dimensional polyhedra that are not pl-homeomorphic [3]. There also exist different pl-structures on certain closed
-dimensional polyhedra that are not pl-homeomorphic [3]. There also exist different pl-structures on certain closed  -manifolds. For
-manifolds. For  , homeomorphic
, homeomorphic  -dimensional polyhedra are pl-homeomorphic. A polyhedron
-dimensional polyhedra are pl-homeomorphic. A polyhedron  is called an
is called an  -dimensional pl-manifold if each point in it has a neighbourhood that is pl-homeomorphic to
-dimensional pl-manifold if each point in it has a neighbourhood that is pl-homeomorphic to 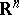 or
or 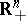 . Any rectilinear triangulation
. Any rectilinear triangulation  of a pl-manifold
of a pl-manifold  is combinatorial. This means that the star at each of its vertices is combinatorially equivalent to a simplex. The Hauptvermutung for polyhedra that are
is combinatorial. This means that the star at each of its vertices is combinatorially equivalent to a simplex. The Hauptvermutung for polyhedra that are  -dimensional topological manifolds naturally splits up into two hypotheses: the hypothesis that any triangulation of such a polyhedron is combinatorial and the Hauptvermutung for pl-manifolds. One of the major achievements in modern topology is that a negative answer has been obtained to both hypotheses for
-dimensional topological manifolds naturally splits up into two hypotheses: the hypothesis that any triangulation of such a polyhedron is combinatorial and the Hauptvermutung for pl-manifolds. One of the major achievements in modern topology is that a negative answer has been obtained to both hypotheses for  [4], [5]. The two hypotheses are true for
[4], [5]. The two hypotheses are true for  .
.
Let  be a compact subpolyhedron of a polyhedron
be a compact subpolyhedron of a polyhedron  and let the pair of geometrical simplicial complexes
and let the pair of geometrical simplicial complexes  triangulate the pair
triangulate the pair 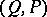 in such a way that
in such a way that 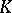 is a complete subcomplex. This means that each simplex of
is a complete subcomplex. This means that each simplex of 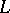 with vertices in
with vertices in 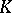 also lies in
also lies in  ; this can always be achieved by passing to a derived subdivision. The polyhedron
; this can always be achieved by passing to a derived subdivision. The polyhedron 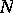 consisting of all closed simplices of a derived subdivision
consisting of all closed simplices of a derived subdivision  having vertices in
having vertices in  is called a regular neighbourhood of
is called a regular neighbourhood of  in
in  , and the same applies to its image under any pl-homeomorphism of
, and the same applies to its image under any pl-homeomorphism of  into itself that leaves
into itself that leaves  invariant. For any two regular neighbourhoods
invariant. For any two regular neighbourhoods  and
and  of
of  there exists a pl-isotopy that leaves
there exists a pl-isotopy that leaves 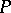 invariant, namely
invariant, namely  , which deforms
, which deforms  to
to  , i.e. is such that
, i.e. is such that  and
and  . One says that the polyhedron
. One says that the polyhedron  is obtained by an elementary polyhedral collapse of a polyhedron
is obtained by an elementary polyhedral collapse of a polyhedron  if for some
if for some  the pair
the pair  is pl-homeomorphic to the pair
is pl-homeomorphic to the pair 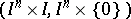 . The polyhedron
. The polyhedron 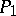 polyhedrally collapses to its subpolyhedron
polyhedrally collapses to its subpolyhedron 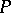 (denoted by
(denoted by  ) if one can pass from
) if one can pass from 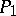 to
to 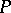 by a finite sequence of elementary polyhedral collapses. If
by a finite sequence of elementary polyhedral collapses. If  , then in a certain triangulation of the pair
, then in a certain triangulation of the pair 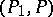 the polyhedron
the polyhedron  can be obtained from
can be obtained from  by a sequence of elementary combinatorial collapses each of which consists in deleting a principal simplex along with its free face. If
by a sequence of elementary combinatorial collapses each of which consists in deleting a principal simplex along with its free face. If  is an
is an  -dimensional pl-manifold, then any regular neighbourhood of a compact polyhedron
-dimensional pl-manifold, then any regular neighbourhood of a compact polyhedron 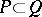 is an
is an  -dimensional pl-manifold and collapses polyhedrally to
-dimensional pl-manifold and collapses polyhedrally to 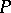 . This property is characteristic: If the
. This property is characteristic: If the  -dimensional pl-manifold
-dimensional pl-manifold  is such that
is such that 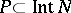 and
and  , then
, then  is a regular neighbourhood in
is a regular neighbourhood in 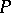 . Any regular neighbourhood of the boundary
. Any regular neighbourhood of the boundary 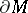 of a compact pl-manifold
of a compact pl-manifold  is pl-homeomorphic to
is pl-homeomorphic to  .
.
Let  and
and  be closed subpolyhedra of an
be closed subpolyhedra of an  -dimensional pl-manifold
-dimensional pl-manifold  ,
, 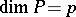 ,
,  . It is said that
. It is said that  and
and 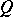 are in general position if
are in general position if  . Any closed subpolyhedra
. Any closed subpolyhedra  may be moved into general position by an arbitrarily small isotopy (cf. Isotopy (in topology)) in
may be moved into general position by an arbitrarily small isotopy (cf. Isotopy (in topology)) in  . This means that for any
. This means that for any  there exists an (
there exists an ( -pl)-isotopy
-pl)-isotopy 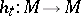 such that the polyhedra
such that the polyhedra  and
and  are in general position. Sometimes one includes conditions of transversality type in the definition of general position. For example, if
are in general position. Sometimes one includes conditions of transversality type in the definition of general position. For example, if  , one can ensure that for each point
, one can ensure that for each point  and a certain neighbourhood
and a certain neighbourhood 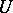 of the point
of the point  in
in 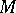 , the triple
, the triple  will be pl-homeomorphic to the triple
will be pl-homeomorphic to the triple 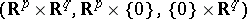 .
.
A curved or topological polyhedron is a topological space  equipped with a homeomorphism
equipped with a homeomorphism  , where
, where 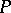 is a polyhedron. The images of the simplices in some triangulation
is a polyhedron. The images of the simplices in some triangulation 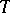 of
of  form a curvilinear triangulation of
form a curvilinear triangulation of 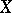 . It is also said that the homeomorphism
. It is also said that the homeomorphism 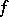 defines a pl-structure on
defines a pl-structure on  . Two pl-structures
. Two pl-structures  ,
,  , coincide if the homeomorphism
, coincide if the homeomorphism  is piecewise linear, and they are isotopic if the homeomorphism
is piecewise linear, and they are isotopic if the homeomorphism  is isotopic to a piecewise-linear one, while they are equivalent if
is isotopic to a piecewise-linear one, while they are equivalent if  and
and  are pl-homeomorphic. For any differentiable manifold
are pl-homeomorphic. For any differentiable manifold  there exists a pl-structure
there exists a pl-structure 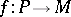 compatible with the differentiable structure on
compatible with the differentiable structure on  . This means that for each closed simplex
. This means that for each closed simplex  of some triangulation of the polyhedron
of some triangulation of the polyhedron  the mapping
the mapping  is differentiable and does not have singular points. Any two such pl-structures in
is differentiable and does not have singular points. Any two such pl-structures in  are isotopic. All the concepts defined for a polyhedron (triangulation, subpolyhedron, regular neighbourhood, and general position) can be transferred by means of the homeomorphism
are isotopic. All the concepts defined for a polyhedron (triangulation, subpolyhedron, regular neighbourhood, and general position) can be transferred by means of the homeomorphism 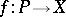 to the curvilinear polyhedron
to the curvilinear polyhedron 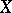 .
.
References
| [1] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
| [2] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
| [3] | J. Milnor, "Two complexes which are homeomorphic but combinatorially distinct" Ann. of Math. , 74 : 3 (1961) pp. 575–590 |
| [4] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) |
| [5] | R.D. Edwards, "The double suspension of a certain homology 3-sphere is 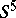 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 |
Comments
Recent developments include: imbedding of topological manifolds as polyhedra with convex (or non-convex) faces in a Euclidean 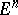 , in particular in
, in particular in 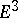 (e.g., polyhedral realizations of regular mappings (i.e. analogues of the regular polyhedra)); polyhedra of given genus with minimal number of vertices or edges or faces; colouring problems; and polyhedral realizations of famous configurations in geometry or topology.
(e.g., polyhedral realizations of regular mappings (i.e. analogues of the regular polyhedra)); polyhedra of given genus with minimal number of vertices or edges or faces; colouring problems; and polyhedral realizations of famous configurations in geometry or topology.
References
| [a1] | U. Brehm, W. Kühnel, "A polyhedral model for Cartan's hypersurfaces in 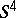 " Mathematika , 33 (1986) pp. 55–61 " Mathematika , 33 (1986) pp. 55–61 |
| [a2] | B. Grünbaum, "Regular polyhedra - old and new" Aequat. Math. , 16 (1977) pp. 1–20 |
| [a3] | P. McMullen, Ch. Schulz, J.M. Wills, "Polyhedral  -manifolds in -manifolds in 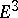 with unusually large genus" Israel J. of Math. , 46 (1983) pp. 127–144 with unusually large genus" Israel J. of Math. , 46 (1983) pp. 127–144 |
| [a4] | E. Schulte, J.M. Wills, "A polyhedral realization of Felix Klein's map 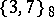 on a Riemann surface of genus 3" J. London Math. Soc. , 32 (1985) pp. 539–547 on a Riemann surface of genus 3" J. London Math. Soc. , 32 (1985) pp. 539–547 |
| [a5] | U. Brehm, "Maximally symmetric polyhedral realizations of Dyck's regular map" Mathematika , 34 (1987) pp. 229–236 |
| [a6] | J.R. Munkres, "Elementary differential topology" , Princeton Univ. Press (1963) |
| [a7] | L.C. Glaser, "Geometrical combinatorial topology" , 1–2 , v. Nostrand (1970) |
Polyhedron, abstract. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polyhedron,_abstract&oldid=11815