Poly-vector
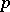 -vector, over a vector space
-vector, over a vector space 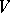
An element of the 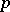 -th exterior degree
-th exterior degree 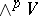 of the space
of the space  over a field
over a field 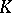 (see Exterior algebra). A
(see Exterior algebra). A  -vector can be understood as a
-vector can be understood as a 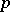 -times skew-symmetrized contravariant tensor on
-times skew-symmetrized contravariant tensor on 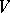 . Any linearly independent system of vectors
. Any linearly independent system of vectors 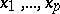 from
from  defines a non-zero
defines a non-zero 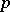 -vector
-vector 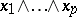 ; such a poly-vector is called factorable, decomposable, pure, or prime (often simply a poly-vector). Here two linearly independent systems
; such a poly-vector is called factorable, decomposable, pure, or prime (often simply a poly-vector). Here two linearly independent systems 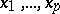 and
and 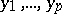 generate the same subspace in
generate the same subspace in 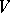 if and only if
if and only if 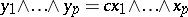 , where
, where 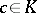 . For any non-zero poly-vector
. For any non-zero poly-vector 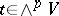 , its annihilator
, its annihilator 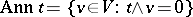 is a subspace of dimension
is a subspace of dimension 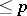 , and the poly-vector
, and the poly-vector 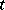 is pure if and only if
is pure if and only if 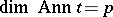 . The pure
. The pure 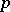 -vectors of an
-vectors of an  -dimensional space
-dimensional space  form an algebraic variety in
form an algebraic variety in 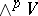 ; the corresponding projective algebraic variety is a Grassmann manifold. Any non-zero
; the corresponding projective algebraic variety is a Grassmann manifold. Any non-zero  -vector or
-vector or 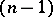 -vector in an
-vector in an  -dimensional space
-dimensional space 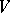 is pure, but a bivector
is pure, but a bivector 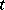 is pure if and only if
is pure if and only if 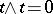 .
.
If  is a basis of
is a basis of 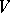 and
and 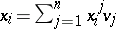 , then the coordinates of the poly-vector
, then the coordinates of the poly-vector 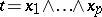 in the basis
in the basis 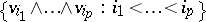 of the space
of the space 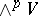 are the minors
are the minors 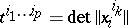 ,
, 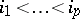 , of the matrix
, of the matrix 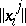 . In particular, for
. In particular, for  ,
,
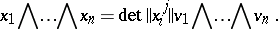 |
If one specifies a non-zero  -vector
-vector 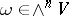 , a duality between
, a duality between 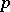 -vectors and
-vectors and 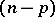 -vectors is obtained, i.e. a natural isomorphism
-vectors is obtained, i.e. a natural isomorphism
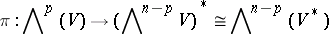 |
such that 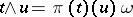 for all
for all 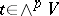 and
and 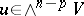 .
.
Let 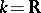 and let an inner product be defined in
and let an inner product be defined in 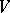 , then in
, then in 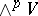 an inner product is induced with the following property: For any orthonormal basis
an inner product is induced with the following property: For any orthonormal basis  in
in 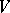 the basis
the basis 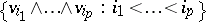 in
in 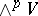 is also orthonormal. The scalar square
is also orthonormal. The scalar square
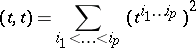 |
of a pure poly-vector 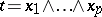 coincides with the square of the volume of the parallelopipedon in
coincides with the square of the volume of the parallelopipedon in 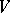 constructed on the vectors
constructed on the vectors 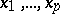 . If one specifies an orientation in the
. If one specifies an orientation in the  -dimensional Euclidean space
-dimensional Euclidean space 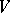 (which is equivalent to choosing an
(which is equivalent to choosing an  -vector
-vector 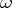 for which
for which 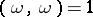 ), then the above duality leads to a natural isomorphism
), then the above duality leads to a natural isomorphism 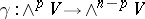 . In particular, the
. In particular, the 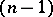 -vector
-vector 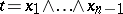 corresponds to a vector
corresponds to a vector  , called the vector product of the vectors
, called the vector product of the vectors 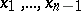 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian) |
| [3] | M.M. Postnikov, "Linear algebra and differential geometry" , Moscow (1979) (In Russian) |
Poly-vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poly-vector&oldid=17085