Pole (of a function)
An isolated singular point  of single-valued character of an analytic function
of single-valued character of an analytic function 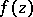 of the complex variable
of the complex variable  for which
for which 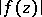 increases without bound when
increases without bound when  approaches
approaches  :
: 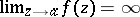 . In a sufficiently small punctured neighbourhood
. In a sufficiently small punctured neighbourhood 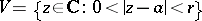 of the point
of the point 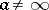 , or
, or 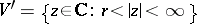 in the case of the point at infinity
in the case of the point at infinity 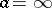 , the function
, the function 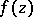 can be written as a Laurent series of special form:
can be written as a Laurent series of special form:
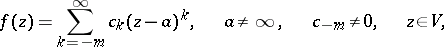 | (1) |
or, respectively,
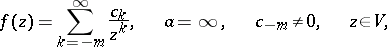 | (2) |
with finitely many negative exponents if 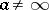 , or, respectively, finitely many positive exponents if
, or, respectively, finitely many positive exponents if 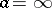 . The natural number
. The natural number 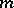 in these expressions is called the order, or multiplicity, of the pole
in these expressions is called the order, or multiplicity, of the pole  ; when
; when 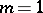 the pole is called simple. The expressions (1) and (2) show that the function
the pole is called simple. The expressions (1) and (2) show that the function 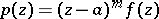 if
if 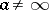 , or
, or 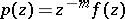 if
if 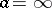 , can be analytically continued (cf. Analytic continuation) to a full neighbourhood of the pole
, can be analytically continued (cf. Analytic continuation) to a full neighbourhood of the pole  , and, moreover,
, and, moreover, 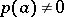 . Alternatively, a pole
. Alternatively, a pole  of order
of order 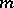 can also be characterized by the fact that the function
can also be characterized by the fact that the function 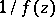 has a zero of multiplicity
has a zero of multiplicity 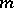 at
at  .
.
A point 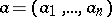 of the complex space
of the complex space 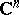 ,
, 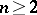 , is called a pole of the analytic function
, is called a pole of the analytic function 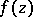 of several complex variables
of several complex variables 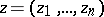 if the following conditions are satisfied: 1)
if the following conditions are satisfied: 1) 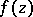 is holomorphic everywhere in some neighbourhood
is holomorphic everywhere in some neighbourhood 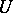 of
of  except at a set
except at a set 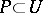 ,
, 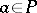 ; 2)
; 2) 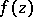 cannot be analytically continued to any point of
cannot be analytically continued to any point of 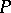 ; and 3) there exists a function
; and 3) there exists a function 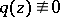 , holomorphic in
, holomorphic in 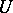 , such that the function
, such that the function 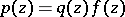 , which is holomorphic in
, which is holomorphic in 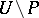 , can be holomorphically continued to the full neighbourhood
, can be holomorphically continued to the full neighbourhood 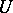 , and, moreover,
, and, moreover, 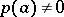 . Here also
. Here also
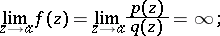 |
however, for 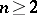 , poles, as with singular points in general, cannot be isolated.
, poles, as with singular points in general, cannot be isolated.
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
Comments
For 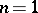 see [a1]. For
see [a1]. For 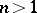 see [a2]–[a3].
see [a2]–[a3].
For the use of poles in the representation of analytic functions see Integral representation of an analytic function; Cauchy integral.
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
| [a2] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German) |
| [a3] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 1, Sect. 3 |
Pole (of a function). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pole_(of_a_function)&oldid=15756