Polarized algebraic variety
A pair 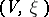 , where
, where 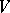 is a complex smooth variety (cf. Algebraic variety) over an algebraically closed field
is a complex smooth variety (cf. Algebraic variety) over an algebraically closed field 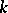 ,
, 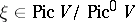 is the class of some ample invertible sheaf (cf. Ample sheaf; Invertible sheaf) and
is the class of some ample invertible sheaf (cf. Ample sheaf; Invertible sheaf) and 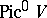 is the connected component of the identity of the Abelian Picard scheme
is the connected component of the identity of the Abelian Picard scheme 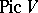 . In the case when
. In the case when  is an Abelian variety, the concept of the degree of polarization of a polarized algebraic variety is also defined: It coincides with the degree of the isogeny
is an Abelian variety, the concept of the degree of polarization of a polarized algebraic variety is also defined: It coincides with the degree of the isogeny 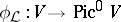 determined by a sheaf
determined by a sheaf 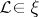 , namely
, namely
 |
where 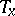 is the morphism of translation by
is the morphism of translation by  ,
, 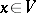 . A polarization of degree one is called a principal polarization.
. A polarization of degree one is called a principal polarization.
The concept of a polarized algebraic variety is closely connected with the concept of a polarized family of algebraic varieties. Let 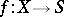 be a family of varieties with base
be a family of varieties with base 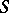 , that is,
, that is, 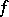 is a smooth projective morphism from the scheme
is a smooth projective morphism from the scheme 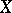 to the Noetherian scheme
to the Noetherian scheme 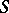 , the fibres of which are algebraic varieties. The pair
, the fibres of which are algebraic varieties. The pair 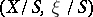 , where
, where 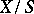 is the family
is the family 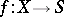 with base
with base 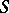 , while
, while 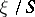 is the class of the relatively-ample invertible sheaf
is the class of the relatively-ample invertible sheaf 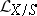 in
in 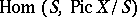 modulo
modulo 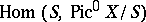 , where
, where 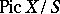 is the relative Picard scheme, is called a polarized family.
is the relative Picard scheme, is called a polarized family.
The introduction of the concept of a polarized family and a polarized algebraic variety is required for the construction of moduli spaces of algebraic varieties (see Moduli theory). For example, there is no moduli space of all smooth algebraic curves of genus 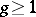 , while for polarized curves there is such a space [4]. One of the first questions connected with the concept of polarization of varieties is the question of simultaneous immersion in a projective space of polarized varieties with numerical invariants. If
, while for polarized curves there is such a space [4]. One of the first questions connected with the concept of polarization of varieties is the question of simultaneous immersion in a projective space of polarized varieties with numerical invariants. If 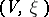 is contained as a fibre in a polarized family
is contained as a fibre in a polarized family 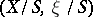 with a connected base
with a connected base 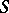 and relatively-ample sheaf
and relatively-ample sheaf  , then does there exist a constant
, then does there exist a constant  depending only on the Hilbert polynomial
depending only on the Hilbert polynomial 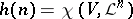 such that for
such that for 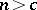 the sheaves
the sheaves 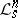 with Hilbert polynomial
with Hilbert polynomial 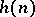 and with
and with 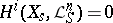 for
for  , are very ample for all polarized algebraic varieties
, are very ample for all polarized algebraic varieties 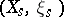 , where
, where 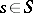 ? For smooth polarized algebraic varieties over an algebraically closed field of characteristic
? For smooth polarized algebraic varieties over an algebraically closed field of characteristic  the answer to this question is affirmative [3], while in the case of surfaces of principal type with the canonical polarization the constant
the answer to this question is affirmative [3], while in the case of surfaces of principal type with the canonical polarization the constant  is even independent of the Hilbert polynomial (see [1], [2]).
is even independent of the Hilbert polynomial (see [1], [2]).
References
| [1] | E. Bombieri, "Canonical models of surfaces of general type" Publ. Math. IHES , 42 (1973) pp. 171–220 |
| [2] | K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" J. Math. Soc. Japan , 20 : 1–2 (1968) pp. 170–192 |
| [3] | T. Matsusaka, D. Mumford, "Two fundamental theorems on deformations of polarized varieties" Amer. J. Math. , 86 : 3 (1964) pp. 668–684 |
| [4] | D. Mumford, "Geometric invariant theory" , Springer (1965) |
Comments
References
| [a1] | D. Mumford, "Matsusaka's big theorem" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 513–530 |
Polarized algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polarized_algebraic_variety&oldid=11345