Polarity
polar transformation
A correlation 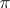 for which
for which 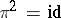 , that is,
, that is, 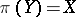 if and only if
if and only if 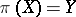 . A polarity divides all subspaces into pairs; in particular, if a pair is formed by the subspaces
. A polarity divides all subspaces into pairs; in particular, if a pair is formed by the subspaces 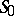 and
and 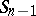 , where
, where 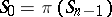 is a point and
is a point and  is a hyperplane, then
is a hyperplane, then 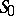 is called the pole of the hyperplane
is called the pole of the hyperplane 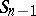 and
and  is called the polar of the point
is called the polar of the point 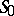 . A projective space
. A projective space 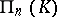 over the skew-field
over the skew-field 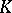 has a polarity if and only if
has a polarity if and only if 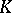 admits an involutory anti-automorphism
admits an involutory anti-automorphism 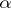 (that is,
(that is, 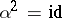 ). Suppose that
). Suppose that 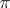 is represented by a semi-bilinear form
is represented by a semi-bilinear form 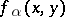 . Then
. Then  is a polarity if and only if
is a polarity if and only if 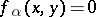 implies
implies 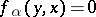 .
.
A polarity 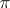 is either a symplectic correlation, characterized by the fact that
is either a symplectic correlation, characterized by the fact that 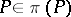 for every point
for every point 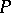 (in this case,
(in this case,  is a skew-symmetric form on
is a skew-symmetric form on 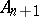 , while
, while 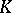 is a field), or
is a field), or 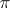 can be represented as an
can be represented as an 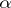 -symmetric form on
-symmetric form on 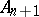 :
: 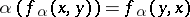 (a symmetric polarity), in this case the existence of a non-strictly isotropic null subspace is equivalent to the fact that the characteristic of the skew-field equals 2 (in particular, if
(a symmetric polarity), in this case the existence of a non-strictly isotropic null subspace is equivalent to the fact that the characteristic of the skew-field equals 2 (in particular, if 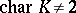 , then any null subspace is strictly isotropic).
, then any null subspace is strictly isotropic).
Relative to a polarity 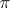 one defines decomposition of a projective space into subspaces, which makes it possible to reduce the semi-bilinear form representing
one defines decomposition of a projective space into subspaces, which makes it possible to reduce the semi-bilinear form representing 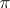 to canonical form. The most important among these are the following:
to canonical form. The most important among these are the following:
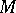 — a maximal non-isotropic null subspace; its dimension is
— a maximal non-isotropic null subspace; its dimension is 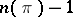 , where
, where  is even and is called the deficiency of
is even and is called the deficiency of 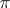 , and
, and 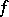 is skew-symmetric;
is skew-symmetric;
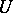 — a maximal strictly-isotropic subspace; its dimension is
— a maximal strictly-isotropic subspace; its dimension is 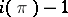 ,
, 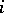 is called the index,
is called the index, 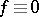 ;
;
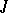 — a component, free or null subspace, non-isotropic, where
— a component, free or null subspace, non-isotropic, where  is positive or negative definite,
is positive or negative definite,  .
.
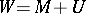 — a maximal null subspace; its dimension is
— a maximal null subspace; its dimension is  .
.
A projective transformation 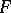 is called
is called 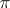 -admissible (relative to the polarity
-admissible (relative to the polarity 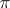 ) if
) if 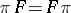 . A semi-linear transformation
. A semi-linear transformation 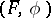 induces a
induces a 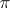 -admissible projective transformation if and only if in
-admissible projective transformation if and only if in 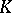 there is a
there is a  for which
for which 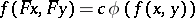 . The
. The 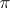 -admissible transformations form a group,
-admissible transformations form a group, 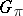 (called the polarity group). If the group
(called the polarity group). If the group 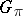 is transitive, either every point of the space
is transitive, either every point of the space 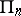 is null (and
is null (and  is called symplectic) or there is no null point (and in this case
is called symplectic) or there is no null point (and in this case 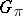 is called orthogonal for
is called orthogonal for 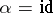 , and unitary for
, and unitary for 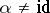 ).
).
References
| [1] | N.V. Efimov, "Higher geometry" , MIR (1980) (Translated from Russian) |
Comments
Let 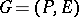 be a bipartite graph, and let
be a bipartite graph, and let 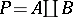 be the corresponding partition of
be the corresponding partition of 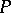 . A polarity on
. A polarity on 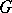 is an automorphism
is an automorphism 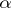 of the graph
of the graph 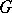 such that
such that 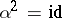 and
and 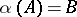 ,
, 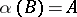 .
.
The term polarity is mostly encountered in a geometric setting such as that of a projective space or incidence system. In this case the two sets of vertices are the lines and points of the incidence structure and there is an edge between a "point-vertex" and a "line-vertex" if and only if the point and line are incident.
The classical setting is that of a projective space 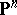 with a non-degenerate bilinear form
with a non-degenerate bilinear form 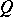 on it. The corresponding polarity between
on it. The corresponding polarity between 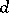 -dimensional subspaces and
-dimensional subspaces and 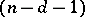 -dimensional subspaces is defined by
-dimensional subspaces is defined by 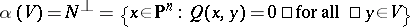 .
.
In the setting of a (Desarguesian or not) projective space  a polarity is also viewed as a symmetric relation
a polarity is also viewed as a symmetric relation 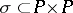 such that for all
such that for all 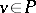 ,
, 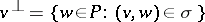 is either a hyperplane or
is either a hyperplane or 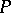 itself. If
itself. If 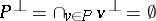 , the polarity is non-degenerate. A subspace
, the polarity is non-degenerate. A subspace 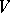 is totally isotropic if
is totally isotropic if 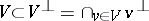 .
.
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) |
| [a3] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a4] | R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) |
| [a5] | D. Pedoe, "Geometry. A comprehensive course" , Dover, reprint (1988) pp. Sect. 85.5 |
| [a6] | P. Dembowsky, "Finite geometries" , Springer (1968) |
Polarity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polarity&oldid=15854