Polar set
The polar set of analytic function 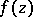 of the complex variable
of the complex variable 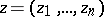 ,
, 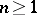 , is the set
, is the set 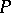 of points in some domain
of points in some domain 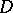 of the complex space
of the complex space 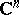 for which: a)
for which: a) 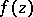 is holomorphic everywhere in
is holomorphic everywhere in 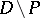 ; b)
; b) 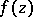 cannot be analytically continued to any point of
cannot be analytically continued to any point of 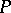 ; and c) for every point
; and c) for every point 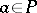 there are a neighbourhood
there are a neighbourhood 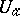 and a function
and a function  , holomorphic in
, holomorphic in 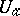 , for which the function
, for which the function 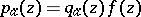 , which is holomorphic in
, which is holomorphic in 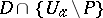 , can be holomorphically continued to
, can be holomorphically continued to 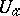 . At every point
. At every point  one has
one has 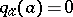 . The polar set
. The polar set 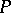 consists of the poles (cf. Pole (of a function))
consists of the poles (cf. Pole (of a function)) 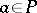 of
of  , for which
, for which 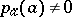 , and the points
, and the points 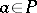 of indeterminacy of
of indeterminacy of 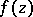 , for which
, for which 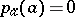 (it is assumed that
(it is assumed that 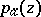 and
and 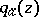 have no common factors that are holomorphic and vanish at
have no common factors that are holomorphic and vanish at  ). Every polar set is an analytic set of complex dimension
). Every polar set is an analytic set of complex dimension 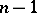 .
.
A polar set in potential theory is a set 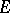 of points of the Euclidean space
of points of the Euclidean space 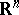 ,
, 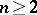 , for which there exists a potential
, for which there exists a potential 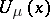 ,
,  , for some Borel measure
, for some Borel measure 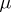 , that takes the value
, that takes the value 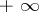 at the points of
at the points of 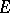 and only at those points.
and only at those points.
In the case of the logarithmic potential for 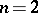 and the Newton potential for
and the Newton potential for 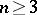 , for a bounded set
, for a bounded set  to be a polar set it is necessary and sufficient that
to be a polar set it is necessary and sufficient that 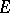 is a set of type
is a set of type 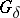 and has zero outer capacity. Here, in the definition of a polar set, one can replace "potential" by "superharmonic function" . The main properties of polar sets in this case are: a) the set
and has zero outer capacity. Here, in the definition of a polar set, one can replace "potential" by "superharmonic function" . The main properties of polar sets in this case are: a) the set 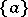 which consists of a single point
which consists of a single point  is a polar set; b) a countable union of polar sets is a polar set; c) any polar set has Lebesgue measure zero in
is a polar set; b) a countable union of polar sets is a polar set; c) any polar set has Lebesgue measure zero in 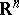 ; and d) under a conformal mapping a polar set goes to a polar set.
; and d) under a conformal mapping a polar set goes to a polar set.
For a local criterion for being polar see Thinness of a set.
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [2] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [3] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Comments
A set 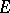 as described under 2) is usually called a complete polar set. A (not necessarily complete) polar set is defined as a subset of a complete polar set. A bounded set is polar if and only if it has zero outer capacity.
as described under 2) is usually called a complete polar set. A (not necessarily complete) polar set is defined as a subset of a complete polar set. A bounded set is polar if and only if it has zero outer capacity.
The sets described under 1) are also called pole sets, or sets of poles, which avoids confusion, cf. [a4] and Meromorphic function.
In parabolic potential theory, a set 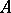 is polar if and only if there exists an open covering
is polar if and only if there exists an open covering 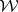 of
of 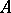 and, for any
and, for any 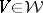 , a positive supercaloric function
, a positive supercaloric function 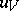 on
on  such that
such that 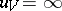 on
on 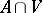 , see [a3]. Again, points are polar and a countable union of polar sets is polar. Any polar set is totally thin but, in contrast with classical potential theory, not every totally thin set is polar. A similar theory of polarity holds in harmonic spaces, see [a2], or in the more general case of balayage spaces, cf. [a1]. In probabilistic potential theory, a Borel set is polar if its first hitting time
, see [a3]. Again, points are polar and a countable union of polar sets is polar. Any polar set is totally thin but, in contrast with classical potential theory, not every totally thin set is polar. A similar theory of polarity holds in harmonic spaces, see [a2], or in the more general case of balayage spaces, cf. [a1]. In probabilistic potential theory, a Borel set is polar if its first hitting time 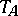 satisfies
satisfies 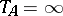 a.s.
a.s.
References
| [a1] | J. Bliedtner, W. Hansen, "Potential theory. An analytic and probabilistic approach to balayage" , Springer (1986) |
| [a2] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [a3] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1983) |
| [a4] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German) |
| [a5] | H. Whitney, "Complex analytic varieties" , Addison-Wesley (1972) pp. Chapt. 8 |
Polar set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar_set&oldid=12257