Polar correspondence
From Encyclopedia of Mathematics
A correspondence between two surfaces such that at corresponding points the radius vector of one of them is parallel to the normal of the other, and vice versa. For every smooth surface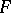 
in 
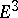with radius vector 
there exists (under certain conditions) a surface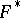 
polar with it and with radius vector 
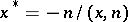, where 
is the normal and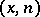 
is the support function to 
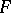, so that
 |
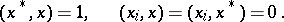Sometimes these conditions are also included in the definition of a polar correspondence.
The concept of polar correspondence shows itself particularly clearly (in the sense of a complete duality) in centro-affine geometry.
How to Cite This Entry:
Polar correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar_correspondence&oldid=14085
Polar correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polar_correspondence&oldid=14085
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article