Poisson summation formula
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The formula
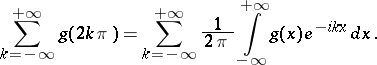 |
The Poisson summation formula holds if, for example, the function 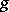 is absolutely integrable on the interval
is absolutely integrable on the interval 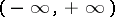 , has bounded variation and
, has bounded variation and 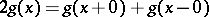 . The Poisson summation formula can also be written in the form
. The Poisson summation formula can also be written in the form
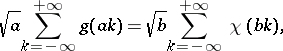 |
where  and
and 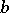 are any two positive numbers satisfying the condition
are any two positive numbers satisfying the condition 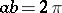 , and
, and 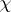 is the Fourier transform of the function
is the Fourier transform of the function 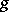 :
:
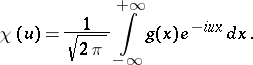 |
References
| [1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [2] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
How to Cite This Entry:
Poisson summation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_summation_formula&oldid=13421
Poisson summation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_summation_formula&oldid=13421
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article