Poisson stability
The property of a point  (a trajectory
(a trajectory  ) of a dynamical system
) of a dynamical system 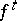 (or
(or 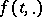 , cf. [2]), given in a topological space
, cf. [2]), given in a topological space 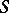 , consisting in the following: There are sequences
, consisting in the following: There are sequences 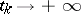 ,
, 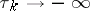 such that
such that
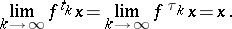 |
In other words,  is an
is an 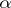 - and
- and 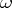 -limit point (cf. Limit point of a trajectory) of the trajectory
-limit point (cf. Limit point of a trajectory) of the trajectory 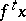 . The concept of Poisson stability was introduced by H. Poincaré [1] on the basis of an analysis of results of Poisson on the stability of planetary orbits.
. The concept of Poisson stability was introduced by H. Poincaré [1] on the basis of an analysis of results of Poisson on the stability of planetary orbits.
Every Poisson-stable point is non-wandering; the converse is not true (cf. Wandering point). Every fixed and every periodic point, more generally, every recurrent point, is Poisson stable. If  and the dynamical system is smooth (i.e. given by a vector field of class
and the dynamical system is smooth (i.e. given by a vector field of class 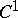 ), then every Poisson-stable point is either fixed or periodic (cf. Poincaré–Bendixson theory).
), then every Poisson-stable point is either fixed or periodic (cf. Poincaré–Bendixson theory).
Poincaré's recurrence theorem (cf. Poincaré return theorem): If a dynamical system is given in a bounded domain of  and if Lebesgue measure is an invariant measure of the system, then all points are Poisson stable, with the exception of a certain set of the first category of measure zero (cf. [1], [3]). A generalization of this theorem to dynamical systems given on a space of infinite measure is the Hopf recurrence theorem (cf. [2]): If a dynamical system is given on an arbitrary domain in
and if Lebesgue measure is an invariant measure of the system, then all points are Poisson stable, with the exception of a certain set of the first category of measure zero (cf. [1], [3]). A generalization of this theorem to dynamical systems given on a space of infinite measure is the Hopf recurrence theorem (cf. [2]): If a dynamical system is given on an arbitrary domain in 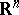 (e.g. on
(e.g. on 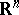 itself) and if Lebesgue measure is an invariant measure of the system, then every point, with the exception of the points of a certain set of measure zero, is either Poisson stable or divergent, i.e.
itself) and if Lebesgue measure is an invariant measure of the system, then every point, with the exception of the points of a certain set of measure zero, is either Poisson stable or divergent, i.e.
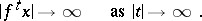 |
There are still more general formulations of the theorems of Poincaré and E. Hopf (cf. [2]).
References
| [1] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 3 , Gauthier-Villars (1899) pp. Chapt. 26 |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | J.C. Oxtoby, "Measure and category" , Springer (1971) |
Comments
In Western literature on (abstract) topological dynamics (as opposed to the qualitative theory of differential equations) often the term "recurrent" is used for Poisson stability; see [a1]. For further comments, see Recurrent point.
References
| [a1] | W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) |
Poisson stability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_stability&oldid=12373