Poisson integral
An integral representation of the solution of the Dirichlet problem for the Laplace equation in the simplest domains. Thus, the Poisson integral for the ball 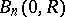 in the Euclidean space
in the Euclidean space 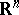 ,
, 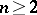 , of radius
, of radius 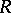 and with centre at the coordinate origin has the form
and with centre at the coordinate origin has the form
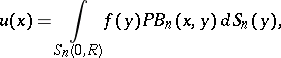 | (1) |
where 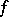 is a given continuous function on the sphere
is a given continuous function on the sphere 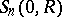 of radius
of radius  ,
,
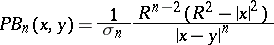 |
is the Poisson kernel for the ball, 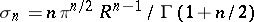 is the area of the sphere
is the area of the sphere 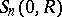 , and
, and  is the surface element on
is the surface element on 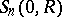 .
.
S.D. Poisson
arrived at formula (1) in the case 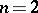 as an integral formula for the sum of the trigonometric series
as an integral formula for the sum of the trigonometric series
 |
where 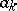 ,
, 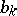 are the Fourier coefficients of the function
are the Fourier coefficients of the function 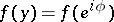 , and
, and 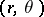 and
and 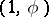 are the polar coordinates of the points
are the polar coordinates of the points 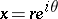 and
and 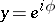 , respectively; in this case the Poisson kernel has the form
, respectively; in this case the Poisson kernel has the form
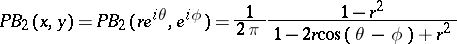 | (2) |
(for applications of the Poisson integral in the theory of trigonometric series see [3] and also Abel–Poisson summation method).
The Poisson integral for the half-space
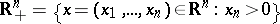 |
has the form
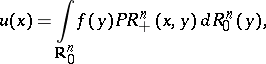 | (3) |
where
 |
 is the volume element in
is the volume element in  ,
,  is a bounded continuous function on
is a bounded continuous function on 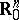 and
and
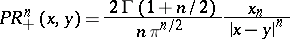 |
is the Poisson kernel for the half-space. The formulas (1) and (3) are particular cases of the Green formula
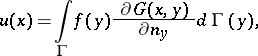 | (4) |
giving the solution of the Dirichlet problem for domains 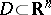 with smooth boundary
with smooth boundary 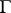 using the derivative
using the derivative 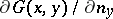 of the Green function
of the Green function 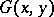 in the direction of the interior normal to
in the direction of the interior normal to 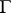 at the point
at the point 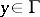 . Sometimes formula (4) is also called the Poisson integral.
. Sometimes formula (4) is also called the Poisson integral.
The basic properties of the Poisson integral are: 1) 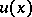 is a harmonic function of the coordinates of the point
is a harmonic function of the coordinates of the point  ; and 2) the Poisson integral gives the solution of the Dirichlet problem with boundary data
; and 2) the Poisson integral gives the solution of the Dirichlet problem with boundary data 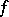 in the class of (bounded) harmonic functions, that is, the function
in the class of (bounded) harmonic functions, that is, the function 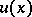 extended to the boundary of the domain by the values
extended to the boundary of the domain by the values 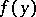 is continuous in the closed domain. Applications of the Poisson integral in classical mathematical physics are based on these properties (see [4]).
is continuous in the closed domain. Applications of the Poisson integral in classical mathematical physics are based on these properties (see [4]).
The Poisson integral understood in the sense of Lebesgue when 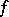 is a summable function, for example on
is a summable function, for example on 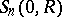 , is called a Poisson–Lebesgue integral; an integral of the form
, is called a Poisson–Lebesgue integral; an integral of the form
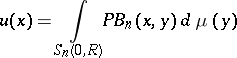 | (5) |
with respect to an arbitrary finite Borel measure  concentrated on
concentrated on 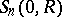 is called a Poisson–Stieltjes integral. The class
is called a Poisson–Stieltjes integral. The class  of harmonic functions
of harmonic functions  representable by an integral (5) is characterized by the fact that any function
representable by an integral (5) is characterized by the fact that any function 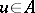 is the difference of two non-negative harmonic functions in
is the difference of two non-negative harmonic functions in 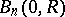 . The class of functions representable by a Poisson–Lebesgue integral is a proper subclass of the class
. The class of functions representable by a Poisson–Lebesgue integral is a proper subclass of the class 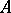 and contains all bounded harmonic functions in
and contains all bounded harmonic functions in 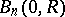 . For almost-all points
. For almost-all points 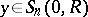 with respect to Lebesgue measure on
with respect to Lebesgue measure on 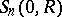 , a Poisson–Stieltjes integral (5) has angular boundary values coinciding with the values of the derivative
, a Poisson–Stieltjes integral (5) has angular boundary values coinciding with the values of the derivative 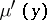 of the measure
of the measure 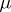 with respect to Lebesgue measure. The theory of Poisson–Stieltjes and Poisson–Lebesgue integrals has also been constructed for the half-space (see [5]).
with respect to Lebesgue measure. The theory of Poisson–Stieltjes and Poisson–Lebesgue integrals has also been constructed for the half-space (see [5]).
Various modifications of the Poisson integral play a large role in the theory of analytic functions of several complex variables and in its applications to quantum field theory. For example, the Poisson kernel for the polydisc
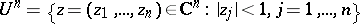 |
in the complex space 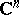 is obtained by multiplying the kernels (2):
is obtained by multiplying the kernels (2):
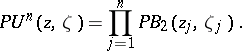 |
The corresponding Poisson integral
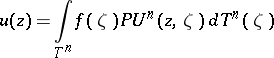 |
with respect to the distinguished boundary 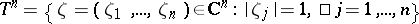 of the polydisc gives a multi-harmonic function
of the polydisc gives a multi-harmonic function 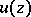 ,
, 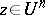 , taking the continuous values
, taking the continuous values 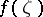 on
on 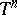 . Generalizations in the form of Poisson–Lebesgue and Poisson–Stieltjes integrals are also considered (see [6]).
. Generalizations in the form of Poisson–Lebesgue and Poisson–Stieltjes integrals are also considered (see [6]).
In quantum field theory Poisson integrals are also applied to tube domains 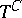 in the complex space
in the complex space  over a convex open acute cone
over a convex open acute cone 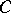 in the space
in the space 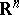 (with vertex at the origin). These have the form
(with vertex at the origin). These have the form
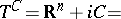 |
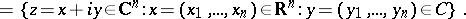 |
A Poisson integral of the form (3) for the half-plane when 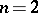 is a particular case of such Poisson integrals for tube domains; the Poisson integral for bounded symmetric domains in the space
is a particular case of such Poisson integrals for tube domains; the Poisson integral for bounded symmetric domains in the space 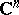 is the same as the Poisson integral for a tube domain in the space of matrices. Taking the density of the Poisson integral
is the same as the Poisson integral for a tube domain in the space of matrices. Taking the density of the Poisson integral 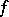 to be a generalized function and the Poisson integral itself to be the convolution of
to be a generalized function and the Poisson integral itself to be the convolution of 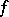 with the Poisson kernel one arrives at the important concept of the Poisson integral for certain classes of generalized functions (see [7]–[9]).
with the Poisson kernel one arrives at the important concept of the Poisson integral for certain classes of generalized functions (see [7]–[9]).
References
| [1a] | S.D. Poisson, J. Ecole R. Polytechn. , 11 (1820) pp. 295–341 |
| [1b] | S.D. Poisson, "Suite du mémoire sur les intégrales définies et sur la sommation des séries" J. Ecole R. Polytechn. , 12 (1823) pp. 404–509 |
| [2] | H.A. Schwarz, "Ueber die Integration der partiellen Differentialgleichung 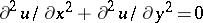 für die Fläche eines Kreises" Vierteljahrsschr. Naturforsch. Ges. Zurich , 15 (1870) pp. 113–128 für die Fläche eines Kreises" Vierteljahrsschr. Naturforsch. Ges. Zurich , 15 (1870) pp. 113–128 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [4] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) |
| [5] | E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie. 1962 (1964) pp. 83–100 (In Russian) |
| [6] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [7] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [8] | L.K. Hua, "Harmonic analysis of functions of several complex variables in the classical domains" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [9] | E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
The Poisson kernel for the exterior of the ball 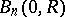 is given by
is given by
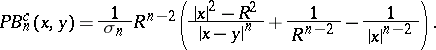 |
In case of the unit ball 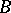 in
in  , there are several Poisson-type kernels, e.g. the classical one, solving the classical Dirichlet problem, and the invariant Poisson kernel, which is invariant under holomorphic automorphisms of the unit ball. It reads
, there are several Poisson-type kernels, e.g. the classical one, solving the classical Dirichlet problem, and the invariant Poisson kernel, which is invariant under holomorphic automorphisms of the unit ball. It reads
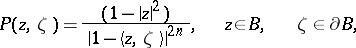 |
where 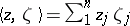 and
and 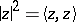 . This is the analogue for the ball of the Poisson kernel with respect to the distinguished boundary of the polydisc, described above. The invariant Poisson kernel solves the Dirichlet problem for the so-called invariant Laplacian, see [a1].
. This is the analogue for the ball of the Poisson kernel with respect to the distinguished boundary of the polydisc, described above. The invariant Poisson kernel solves the Dirichlet problem for the so-called invariant Laplacian, see [a1].
References
| [a1] | W. Rudin, "Function theory in the unit ball in  " , Springer (1980) " , Springer (1980) |
Poisson integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_integral&oldid=18887