Poisson formula for harmonic functions

Consider a harmonic function defined in a domain in a Euclidean space , . Let denote the open ball

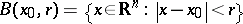with centre and radius . Assume that the closure of this ball is contained in .

The classical Poisson formula expresses that 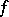can be recovered inside the ball by the values of on the boundary of the ball integrated against the Poisson kernel for the ball,

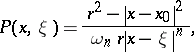(a1)

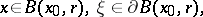where

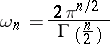is the 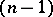-dimensional surface area of the unit ball in .

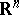The Poisson formula is

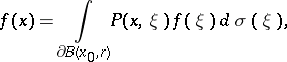where 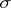is the surface measure of the ball, the total mass of which is .

For the formula reduces to the mean-value theorem for harmonic functions, stating that the value at the centre of the ball is the average over the boundary of the ball.

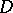The same type of formula holds when the ball is replaced by a bounded domain with a sufficiently smooth boundary and such that the closure of is contained in . The Poisson kernel (a1) is replaced by the Poisson kernel 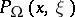for and 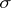is replaced by the surface measure on the boundary of . The Poisson kernel, defined on 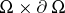, is given as

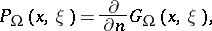where the inward normal derivative of the Green function for with respect to the second variable 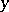is used.

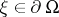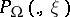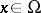For each the function is positive and harmonic in , and for each the measure

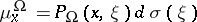is a probability, called the harmonic measure for at .

The Poisson kernel has the properties ()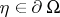

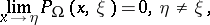and

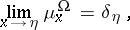where the last limit is in the weak topology for probability measures on (cf. also Weak convergence of probability measures) and 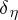is the Dirac distribution at .

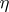There are only a few cases where the Poisson kernel can be given in closed form as for the ball.

The Poisson formula for a domain is related to the solution of the Dirichlet problem: For a function 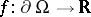, the harmonic continuation in is (under suitable assumptions) given as

There is also a Poisson formula for unbounded domains, the simplest of which is for the upper half-space

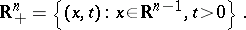The formula is

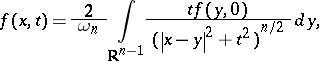and it is valid for a harmonic function 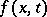in the upper half-space provided it has a continuous extension to the closure and satisfies some growth condition. See Hardy spaces.

References

[a1]	J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984)