Poisson equation
A partial differential equation which is satisfied by the potential of a mass distribution inside domains occupied by the masses creating this potential. For the Newton potential in the space 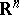 ,
, 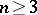 , and the logarithmic potential in
, and the logarithmic potential in  the Poisson equation has the form
the Poisson equation has the form
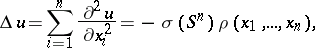 |
where 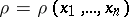 is the density of the mass distribution,
is the density of the mass distribution, 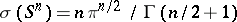 is the area of the unit sphere
is the area of the unit sphere 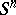 in
in 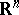 and
and 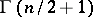 is the value of the gamma-function.
is the value of the gamma-function.
Poisson's equation is a basic example of a non-homogeneous equation of elliptic type. The equation was first considered by S. Poisson (1812).
References
| [1] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [2] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
Comments
The map 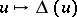 defines a morphism from the sheaf of local differences of superharmonic functions into a sheaf of measures on
defines a morphism from the sheaf of local differences of superharmonic functions into a sheaf of measures on 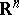 . This remark leads to a treatment of the Poisson problem in the framework of harmonic spaces (cf. Harmonic space), see [a1].
. This remark leads to a treatment of the Poisson problem in the framework of harmonic spaces (cf. Harmonic space), see [a1].
References
| [a1] | F.-Y. Maeda, "Dirichlet integrals on harmonic spaces" , Lect. notes in math. , 803 , Springer (1980) |
| [a2] | S.D. Poisson, "Remarques sur une équation qui se présente dans la théorie des attractions des sphéroïdes" Nouveau Bull. Soc. Philomathique de Paris , 3 (1813) pp. 388–392 |
| [a3] | W. Rudin, "Function theory in the unit ball in 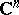 " , Springer (1980) " , Springer (1980) |
| [a4] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
Poisson equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_equation&oldid=28262