Poisson distribution
A probability distribution of a random variable 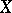 taking non-negative integer values
taking non-negative integer values 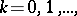 with probabilities
with probabilities
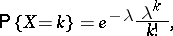 |
where 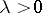 is a parameter. The generating function and the characteristic function of the Poisson distribution are defined by
is a parameter. The generating function and the characteristic function of the Poisson distribution are defined by
 |
respectively. The mean, variance and the semi-invariants of higher order are all equal to 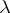 . The distribution function of the Poisson distribution,
. The distribution function of the Poisson distribution,
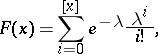 |
is given at the points 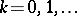 by
by
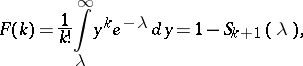 |
where 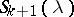 is the value at the point
is the value at the point 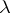 of the gamma-distribution function with parameter
of the gamma-distribution function with parameter 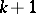 (or by
(or by 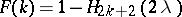 , where
, where 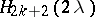 is the value at the point
is the value at the point 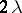 of the "chi-squared" distribution function with
of the "chi-squared" distribution function with 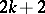 degrees of freedom) whence, in particular,
degrees of freedom) whence, in particular,
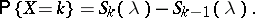 |
The sum of independent variables 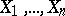 each having a Poisson distribution with parameters
each having a Poisson distribution with parameters 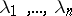 has a Poisson distribution with parameter
has a Poisson distribution with parameter 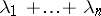 .
.
Conversely, if the sum 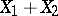 of two independent random variables
of two independent random variables 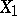 and
and 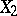 has a Poisson distribution, then each random variable
has a Poisson distribution, then each random variable 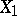 and
and 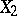 is subject to a Poisson distribution (Raikov's theorem). There are general necessary and sufficient conditions for the convergence of the distribution of sums of independent random variables to a Poisson distribution. In the limit, as
is subject to a Poisson distribution (Raikov's theorem). There are general necessary and sufficient conditions for the convergence of the distribution of sums of independent random variables to a Poisson distribution. In the limit, as 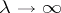 , the random variable
, the random variable 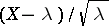 has the standard normal distribution.
has the standard normal distribution.
The Poisson distribution was first obtained by S. Poisson (1837) when deriving approximate formulas for the binomial distribution when  (the number of trials) is large and
(the number of trials) is large and 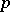 (the probability of success) is small. See Poisson theorem 2). The Poisson distribution describes many physical phenomena with good approximation (see [2], Vol. 1, Chapt. 6). The Poisson distribution is the limiting case for many discrete distributions such as, for example, the hypergeometric distribution, the negative binomial distribution, the Pólya distribution, and for the distributions arising in problems about the arrangements of particles in cells with a given variation in the parameters. The Poisson distribution also plays an important role in probabilistic models as an exact probability distribution. The nature of the Poisson distribution as an exact probability distribution is discussed more fully in the theory of random processes (see Poisson process), where the Poisson distribution appears as the distribution of the number
(the probability of success) is small. See Poisson theorem 2). The Poisson distribution describes many physical phenomena with good approximation (see [2], Vol. 1, Chapt. 6). The Poisson distribution is the limiting case for many discrete distributions such as, for example, the hypergeometric distribution, the negative binomial distribution, the Pólya distribution, and for the distributions arising in problems about the arrangements of particles in cells with a given variation in the parameters. The Poisson distribution also plays an important role in probabilistic models as an exact probability distribution. The nature of the Poisson distribution as an exact probability distribution is discussed more fully in the theory of random processes (see Poisson process), where the Poisson distribution appears as the distribution of the number 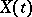 of certain random events occurring in the course of time
of certain random events occurring in the course of time 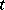 in a fixed interval:
in a fixed interval:
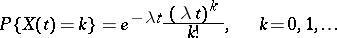 |
(the parameter 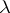 is the mean number of events in unit time), or, more generally, as the distribution of a random number of points in a certain fixed domain of Euclidean space (the parameter of the distribution is proportional to the volume of the domain).
is the mean number of events in unit time), or, more generally, as the distribution of a random number of points in a certain fixed domain of Euclidean space (the parameter of the distribution is proportional to the volume of the domain).
Along with the Poisson distribution, as defined above, one considers the so-called generalized or compound Poisson distribution. This is the probability distribution of the sum 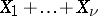 of a random number
of a random number  of identically-distributed random variables
of identically-distributed random variables 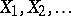 (where
(where 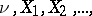 are considered to be mutually independent and
are considered to be mutually independent and  is distributed according to the Poisson distribution with parameter
is distributed according to the Poisson distribution with parameter 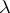 ). The characteristic function
). The characteristic function 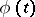 of the compound Poisson distribution is
of the compound Poisson distribution is
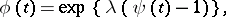 |
where 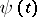 is the characteristic function of
is the characteristic function of 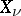 . For example, the negative binomial distribution with parameters
. For example, the negative binomial distribution with parameters  and
and 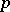 is a compound Poisson distribution, since one can put
is a compound Poisson distribution, since one can put
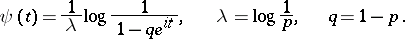 |
The compound Poisson distributions are infinitely divisible and every infinitely-divisible distribution is a limit of compound Poisson distributions (perhaps "shifted" , that is, with characteristic functions of the form 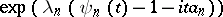 ). In addition, the infinitely-divisible distributions (and these alone) can be obtained as limits of the distributions of sums of the form
). In addition, the infinitely-divisible distributions (and these alone) can be obtained as limits of the distributions of sums of the form 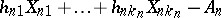 , where
, where 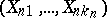 form a triangular array of independent random variables each with a Poisson distribution, and where
form a triangular array of independent random variables each with a Poisson distribution, and where 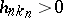 and
and  are real numbers.
are real numbers.
References
| [1] | S.D. Poisson, "Récherches sur la probabilité des jugements en matière criminelle et en matière civile" , Paris (1837) |
| [2] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1950–1966) |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [4] | Yu.V. Linnik, I.V. Ostrovskii, "Decomposition of random variables and vectors" , Amer. Math. Soc. (1977) (Translated from Russian) |
Comments
The Poisson distribution frequently occurs in queueing theory.
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics: discrete distributions" , Houghton Mifflin (1970) |
Poisson distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_distribution&oldid=18030