Poisson brackets

The differential expression

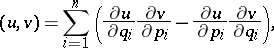(1)

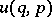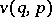depending on two functions and of 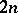variables 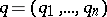, 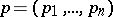. The Poisson brackets, introduced by S. Poisson [1], are a particular case of the Jacobi brackets. The Poisson brackets are a bilinear form in the functions and , such that

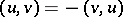and the Jacobi identity

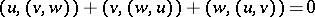holds (see [2]).

The Poisson brackets are used in the theory of first-order partial differential equations and are a useful mathematical tool in analytical mechanics (see [3]–[5]). For example, if 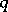and 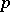are canonical variables and a transformation

(2)

is given, where 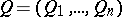, 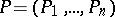and the 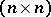-matrices

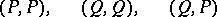(3)

are constructed with entries 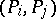, , 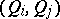, 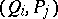respectively, then (2) is a canonical transformation if and only if the first two matrices in (3) are zero and the third is the unit matrix.

The Poisson brackets, computed for the case when and are replaced in (1) by some pair of coordinate functions in 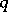and 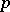, are also called fundamental brackets.

References

[1]	S. Poisson, J. Ecole Polytechn. , 8 (1809) pp. 266–344
[2]	C.G.J. Jacobi, "Nova methodus, aequationes differentiales partiales primi ordinis inter numurum variabilium quemcunque propositas integrandi" J. Reine Angew. Math. , 60 (1862) pp. 1–181
[3]	E.T. Whittaker, "Analytical dynamics of particles and rigid bodies" , Dover, reprint (1944)
[4]	A.I. Lur'e, "Analytical mechanics" , Moscow (1961) (In Russian)
[5]	H. Goldstein, "Classical mechanics" , Addison-Wesley (1957)

Comments

Other basic properties of Poisson brackets are invariance under canonical transformations and the fact that 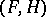expresses the derivative of 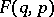along trajectories, if 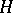is the Hamiltonian, so that the corresponding Hamiltonian equations are 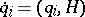, , 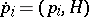which for a "standard" Hamiltonian of the form 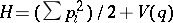gives back , 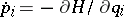. Therefore 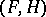expresses a conservation law, i.e. 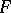is a conserved quantity.

The Poisson brackets may be defined for functionals depending on a function 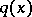, as

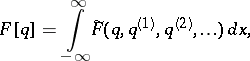with .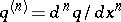

One has

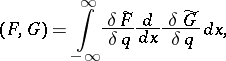with , 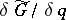variational derivatives, i.e.

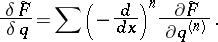References

[a1]	A.C. Newell, "Solitons in mathematical physics" , SIAM (1985)
[a2]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)
[a3]	R. Abraham, J.E. Marsden, "Foundations of mechanics" , Benjamin (1978)
[a4]	F.R. [F.R. Gantmakher] Gantmacher, "Lectures in analytical mechanics" , MIR (1975) (Translated from Russian)