Poincaré return theorem
One of the basic theorems in the general theory of dynamical systems with an invariant measure (cf. also Ergodic theory).
Let the motion of a system be described by the differential equations
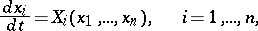 | (1) |
where the single-valued functions 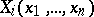 satisfy the condition
satisfy the condition
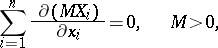 |
so that equations (1) admit a positive integral invariant
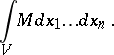 | (2) |
It is also assumed that if there exists a certain domain  of finite volume such that if a moving point
of finite volume such that if a moving point  with coordinates
with coordinates  is found inside
is found inside 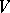 at the initial moment of time
at the initial moment of time 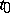 , then it will remain inside this domain for an arbitrary long time and
, then it will remain inside this domain for an arbitrary long time and
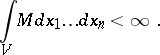 |
The Poincaré return theorem: If one considers a domain 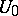 contained in
contained in 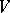 , then there is an infinite choice of initial positions of the point
, then there is an infinite choice of initial positions of the point 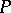 such that the trajectory of
such that the trajectory of 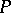 intersects the domain
intersects the domain 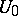 an infinite number of times. If this choice of the initial position is made at random inside
an infinite number of times. If this choice of the initial position is made at random inside 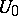 , then the probability that the point
, then the probability that the point 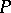 does not intersect the domain
does not intersect the domain 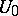 an infinite number of times will be infinitely small.
an infinite number of times will be infinitely small.
In other words, if the initial conditions are not exceptional in the sense indicated, then the point  passes infinitely often arbitrarily near to its initial position.
passes infinitely often arbitrarily near to its initial position.
H. Poincaré called a motion in which the system returns an infinite number of times to a neighbourhood of the initial state stable in the sense of Poisson (see Poisson stability). The Poincaré return theorem was first established by Poincaré (see [1] and [2]) and its proof was improved by C. Carathéodory [3].
Carathéodory used four axioms to introduce the abstract concept of the measure 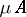 of any set
of any set 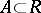 of a metric space
of a metric space 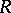 , and considered a dynamical system
, and considered a dynamical system 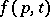 (
(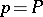 for
for  ) in
) in 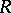 ; he then called the measure invariant with respect to the system
; he then called the measure invariant with respect to the system 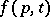 if for any
if for any 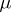 -measurable set
-measurable set  ,
,
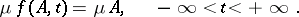 |
An invariant measure is the natural generalization of the integral invariants (2) for the differential equations (1). Assuming the measure of the whole space 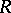 to be finite, Carathéodory proved that:
to be finite, Carathéodory proved that:
1) if 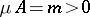 , then values
, then values  can be found,
can be found, 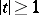 , such that
, such that 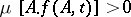 , where
, where 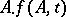 is the set of points belonging simultaneously to the sets
is the set of points belonging simultaneously to the sets 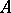 and
and  ;
;
2) if in a space 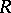 with a countable base,
with a countable base, 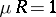 for the invariant measure
for the invariant measure 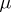 , then almost-all points
, then almost-all points 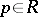 (in the sense of the measure
(in the sense of the measure  ) are stable in the sense of Poisson.
) are stable in the sense of Poisson.
A.Ya. Khinchin [5] made part 1) of this theorem more precise by proving that for each measurable set 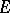 ,
, 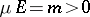 , and for any
, and for any  ,
, 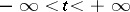 , the inequality
, the inequality
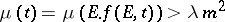 |
is satisfied for a relatively-dense set of values of 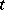 on the axis
on the axis  (for any
(for any 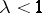 ).
).
N.G. Chetaev (see [6], [7]) generalized Poincaré's theorem for the case when the functions 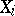 in (1) depend also periodically on the time
in (1) depend also periodically on the time  . Namely, let a) only real values of variables correspond to the real states of the system; b) the functions
. Namely, let a) only real values of variables correspond to the real states of the system; b) the functions 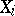 in the differential equations (1) of the motion be periodic with respect to
in the differential equations (1) of the motion be periodic with respect to 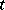 with a single period
with a single period  common to them all; c) throughout its motion, the point
common to them all; c) throughout its motion, the point  does not leave a certain closed domain
does not leave a certain closed domain  if its initial position
if its initial position  is somewhere inside a given domain
is somewhere inside a given domain 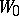 ; d)
; d) 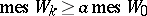 , where
, where 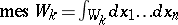 denotes the measure of the set
denotes the measure of the set  (volume in the sense of Lebesgue) which consists of those moving points at time
(volume in the sense of Lebesgue) which consists of those moving points at time 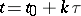 which started at time
which started at time 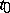 from
from 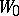 ;
; 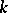 is a certain integer, and it is assumed that the constant
is a certain integer, and it is assumed that the constant  is not infinitesimally small. Then almost-everywhere in the domain
is not infinitesimally small. Then almost-everywhere in the domain  (apart perhaps on a set of measure zero) the trajectories are stable in the sense of Poisson.
(apart perhaps on a set of measure zero) the trajectories are stable in the sense of Poisson.
N.M. Krylov and N.N. Bogolyubov [8] described the structure of the invariant measure with respect to the given dynamical system for a very wide class of dynamical systems (see also [4]).
References
| [1] | H. Poincaré, "Sur le problème des trois corps et les équations de la dynamique" Acta. Math. , 13 (1890) pp. 1–270 |
| [2] | H. Poincaré, "Sur le problème des trois corps et les équations de la dynamique" , Oeuvres , XII , Gauthier-Villars (1952) pp. 262–479 (in particular, p. 314) |
| [3] | C. Carathéodory, "Ueber den Wiederkehrsatz von Poincaré" Sitz. Ber. Preuss. Akad. Wiss. Berlin (1919) pp. 580–584 |
| [4] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [5] | A.Ya. Khinchin, "Eine Verschärfung des Poincaréschen Wiederkehrsatzes" Comp. Math. , 1 (1934) pp. 177–179 |
| [6] | N.G. Chetaev, "Sur la stabilité à la Poisson" C.R. Acad. Sci. Paris , 187 (1928) pp. 637–638 |
| [7] | N.G. Chetaev, Uchen. Zap. Kazan. Univ. , 89 : 2 (1929) pp. 199–201 |
| [8] | N.N. Krylov, N.N. Bogolyubov, "La théorie de la mesure dans son application à l'etude des systèmes dynamiques de la mécanique non-linéaire" Ann. of Math. , 38 : 1 (1937) pp. 65–113 |
Comments
In the literature the result discussed above is also often called the Poincaré recurrence theorem.
The set 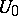 in the theorem need not be open: the theorem is true provided only that
in the theorem need not be open: the theorem is true provided only that 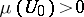 . The recurrence theorem is valid for volume-preserving flows on Riemannian manifolds
. The recurrence theorem is valid for volume-preserving flows on Riemannian manifolds 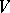 of finite volume. The recurrence theorem is also true for a discrete-time dynamical system, e.g. for a mapping
of finite volume. The recurrence theorem is also true for a discrete-time dynamical system, e.g. for a mapping 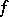 of a bounded domain in Euclidean space to itself that preserves Lebesgue measure. See [a1] for another generalization.
of a bounded domain in Euclidean space to itself that preserves Lebesgue measure. See [a1] for another generalization.
There seems to be an incompatibility of the prediction by Poincaré's recurrence theorem (namely, almost surely a system will recur arbitrarily close to its original state) with the conclusions of thermodynamics as the second law and the Boltzmann 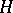 -theorem (increasing entropy). In this respect the following estimation of the expected recurrence time is of interest: it is
-theorem (increasing entropy). In this respect the following estimation of the expected recurrence time is of interest: it is 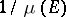 , where
, where 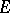 denotes the "event" that recurs
denotes the "event" that recurs 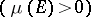 ; for practical situations this time is much larger than the lifetime of the universe (by factors like
; for practical situations this time is much larger than the lifetime of the universe (by factors like 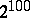 ); see [a2].
); see [a2].
The Poincaré recurrence theorem was used by S. Kakutani as the basis for an important construction: that of the induced or derivative transformation of a measure-preserving transformation (with as a reverse construction that of a primitive transformation). See [a3] or [a4], pp. 39, 40.
References
| [a1] | P.R. Halmos, "Invariant measures" Ann. of Math. , 48 (1947) pp. 735–754 |
| [a2] | M. Kac, "On the notion of recurrence in discrete stochastic processes" Bull. Amer. Math. Soc. , 53 (1947) pp. 1002–1010 |
| [a3] | S. Kakutani, "Induced measure preserving transformations" Proc. Japan. Acad. , 19 (1943) pp. 635–641 |
| [a4] | K. Petersen, "Ergodic theory" , Cambridge Univ. Press (1983) pp. 39 |
Poincaré return theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_return_theorem&oldid=12573