Difference between revisions of "Poincaré divisor"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Poincaré divisor to Poincare divisor: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
The divisor given by the natural polarization over the Jacobian (cf. Jacobi variety) of an algebraic curve. The intersection form of one-dimensional cycles in the homology of an algebraic curve 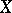 induces a unimodular skew-symmetric form on the lattice of periods. By the definition of a polarized Abelian variety (cf. Polarized algebraic variety) this form determines the principal polarization over the Jacobian
induces a unimodular skew-symmetric form on the lattice of periods. By the definition of a polarized Abelian variety (cf. Polarized algebraic variety) this form determines the principal polarization over the Jacobian 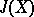 of the curve. Therefore the effective divisor
of the curve. Therefore the effective divisor 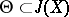 given by this polarization is uniquely determined up to translation by an element
given by this polarization is uniquely determined up to translation by an element  . The geometry of the Poincaré divisor
. The geometry of the Poincaré divisor 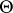 reflects the geometry of the algebraic curve
reflects the geometry of the algebraic curve 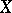 . In particular, the set of singular points of the Poincaré divisor has dimension
. In particular, the set of singular points of the Poincaré divisor has dimension  , where
, where 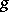 is the genus of the curve
is the genus of the curve 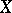 (see [1]).
(see [1]).
References
| [1] | A. Andreotti, A. Mayer, "On period relations for abelian integrals on algebraic curves" Ann. Sci. Scuola Norm. Sup. Pisa , 21 : 2 (1967) pp. 189–238 |
Comments
The above divisor is usually called the theta divisor of the Jacobi variety. For the rich geometry connected with it see, for instance, the books [a1], [a2] and [a3] and the survey articles [a4] and [a5].
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [a2] | D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1975) |
| [a3] | E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985) |
| [a4] | E. Arbarello, "Fay's triscant formula and a characterisation of Jacobian varieties" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 , Amer. Math. Soc. (1987) pp. 49–61 |
| [a5] | R.C. Gunning, "On theta functions for Jacobi varieties" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 , Amer. Math. Soc. (1987) pp. 89–98 |
Poincaré divisor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_divisor&oldid=12934