Po-group
partially ordered group
A group 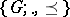 endowed with a partial order
endowed with a partial order 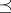 such that for all
such that for all 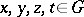 ,
,
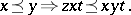 |
(Cf. also Partially ordered group.) If  is the identity of a
is the identity of a 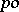 -group
-group 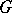 and
and 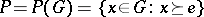 is the positive cone of
is the positive cone of 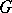 (cf.
(cf. 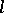 -group), then the following relations hold:
-group), then the following relations hold:
1) 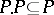 ;
;
2) 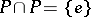 ;
;
3) 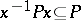 for all
for all  .
.
If, in a group 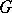 , one can find a set
, one can find a set 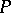 with the properties 1)–3), then
with the properties 1)–3), then 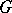 can be made into a
can be made into a 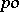 -group by setting
-group by setting 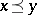 if and only if
if and only if 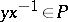 . It is correct to identify the order of a
. It is correct to identify the order of a  -group with its positive cone. One often writes a
-group with its positive cone. One often writes a  -group
-group 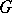 with positive cone
with positive cone 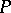 as
as 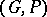 .
.
A mapping 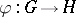 from a
from a 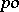 -group
-group 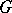 into a
into a 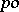 -group
-group 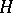 is an order homomorphism if
is an order homomorphism if 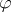 is a homomorphism of the group
is a homomorphism of the group 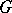 and for all
and for all 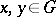 ,
,
 |
A homomorphism 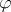 from a
from a 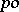 -group
-group 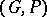 into a
into a 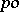 -group
-group 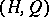 is an order homomorphism if and only if
is an order homomorphism if and only if 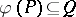 .
.
A subgroup 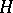 of a
of a 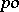 -group
-group 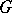 is called convex (cf. Convex subgroup) if for all
is called convex (cf. Convex subgroup) if for all 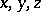 with
with 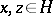 ,
,
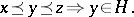 |
If 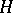 is a convex subgroup of a
is a convex subgroup of a 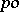 -group
-group 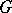 , then the set
, then the set 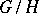 of right cosets of
of right cosets of 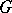 by
by 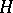 is a partially ordered set with the induced order
is a partially ordered set with the induced order 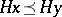 if there exists an
if there exists an 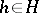 such that
such that 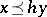 . The quotient group
. The quotient group  of a
of a  -group
-group 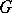 by a convex normal subgroup
by a convex normal subgroup 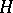 is a
is a 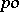 -group respect with the induced partial order, and the natural homomorphism
-group respect with the induced partial order, and the natural homomorphism 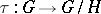 is an order homomorphism. The homomorphism theorem holds for
is an order homomorphism. The homomorphism theorem holds for 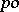 -groups: if
-groups: if 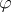 is an order homomorphism from a
is an order homomorphism from a 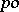 -group
-group 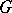 into a
into a 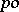 -group
-group 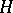 , then the kernel
, then the kernel  of
of 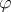 is a convex normal subgroup of
is a convex normal subgroup of 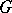 and there exists an order isomorphism
and there exists an order isomorphism 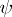 from the
from the 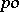 -group
-group 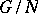 into
into 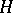 such that
such that 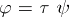 .
.
The most important classes of 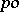 -groups are the class of lattice-ordered groups (cf.
-groups are the class of lattice-ordered groups (cf.  -group) and the class of totally ordered groups (cf.
-group) and the class of totally ordered groups (cf.  -group).
-group).
This article extends and updates the article Partially ordered group (Volume 7).
References
| [a1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
Po-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Po-group&oldid=48197