Pluripotential theory
The natural brand of potential theory in the setting of function theory of several complex variables (cf. also Analytic function). The basic objects are plurisubharmonic functions (cf. also Plurisubharmonic function). These are studied much from the same perspective as subharmonic functions (cf. also Subharmonic function) are studied in potential theory on ${\bf R} ^ { n }$. General references are [a1], [a10], [a16], [a23].
A function $u$ on a domain $D \subset \mathbf{C} ^ { x }$ is called plurisubharmonic if it is subharmonic on $D$, viewed as a domain in $\mathbf{R} ^ { 2 n }$, and if the restriction of $u$ to every complex line in $D$ is subharmonic (cf. also Plurisubharmonic function; Subharmonic function). If $u$ is $C ^ { 2 }$ on a domain $D \subset \mathbf{C} ^ { x }$, then $u$ is plurisubharmonic if and only if
\begin{equation*} \left( \frac { \partial ^ { 2 } u } { \partial z _ { i } \partial \overline{z _ { j } }} \right) \end{equation*}
is a non-negative Hermitian matrix on $D$. One denotes the set of plurisubharmonic functions on a domain $D \subset \mathbf{C} ^ { x }$ by $\operatorname{PSH} ( D )$. Plurisubharmonic functions can be defined on domains in complex manifolds via local coordinates (cf. also Analytic manifold).
Plurisubharmonic functions are precisely the subharmonic functions invariant under a holomorphic change of coordinates. If $f$ is holomorphic on a domain $D$ in $\mathbf{C} ^ { n }$ (cf. also Analytic function), then $\operatorname { log } | f |$ is plurisubharmonic on $D$. Moreover, every plurisubharmonic function can locally be written as
\begin{equation*} \operatorname { limsup } _ { j \rightarrow \infty } \frac { 1 } { j } \operatorname { log } | f _ { j } |, \end{equation*}
for suitable holomorphic functions $f_j$, see [a7]. Plurisubharmonic functions were formally introduced by P. Lelong, [a19], and K. Oka, [a22], although related ideas stem from the end of the nineteenth century.
The analogue of the Laplace operator on domains in $\mathbf{C}$ is the Monge–Ampère operator:
\begin{equation*} M f = \operatorname { det } \left( \frac { \partial ^ { 2 } f } { \partial z _ { i } \partial \overline{z}_ { j } } \right) . \end{equation*}
This operator is originally only defined for $C ^ { 2 }$ plurisubharmonic functions (cf. also Monge–Ampère equation). Due to the non-linearity of $M$ it is impossible to extend it to a well-defined operator on all plurisubharmonic functions on a domain $D$ in such a way that $\operatorname { lim } _ { n \rightarrow \infty } M ( u _ { n } ) = M ( u )$ if $\{ u _ { n } \}$ is a decreasing sequence of plurisubharmonic functions with limit $u$, see [a9]. Nevertheless, the domain of $M$ can be enlarged to include all bounded plurisubharmonic functions, [a3]. The most recent result (as of 2000) in this direction is in [a11].
On strongly pseudo-convex domains $D$ (cf. also Pseudo-convex and pseudo-concave), the following Dirichlet problem for the Monge–Ampère operator was solved by E. Bedford and B.A. Taylor [a3]: Given $f$ continuous on $\partial D$ and $\phi$ continuous on $D$, there exists a continuous plurisubharmonic function $u$ on $D$, continuous up to the boundary of $D$, such that
\begin{equation} \tag{a1} \left\{ \begin{array} { c } { M ( u ) = \phi } & {\text { on } D , } \\ { u |_{ \partial D = f.} } \end{array} \right. \end{equation}
This result has been extended by weakening the conditions on $D$, and replacing $\phi$ by certain positive measures; see e.g. [a5], [a18]. In [a11], large classes of plurisubharmonic functions on which the Monge–Ampère operator is well defined are determined and necessary and sufficient conditions on a positive measure $\phi$ are given, so that the problem (a1) has a solution within such a class.
The regularity of this Dirichlet problem is quite bad. The following example is due to T. Gamelin and N. Sibony: Let $D$ be the unit ball in $\mathbf{C} ^ { 2 }$,
\begin{equation*} f ( z _ { 1 } , z _ { 2 } ) = \left( | z _ { 1 } | ^ { 2 } - \frac { 1 } { 2 } \right) ^ { 2 } = \left( | z _ { 2 } | ^ { 2 } - \frac { 1 } { 2 } \right) ^ { 2 }, \end{equation*}
\begin{equation*} ( z _ { 1 } , z _ { 2 } ) \in \partial D. \end{equation*}
Then the function
\begin{equation*} u ( z _ { 1 } , z _ { 2 } ) = \left\{ \begin{array} { c l } { 0 } & { \text { if } | z _ { 1 } | ^ { 2 } , | z _ { 2 } | ^ { 2 } < \frac { 1 } { 2 } } ,\\ { \operatorname { max } \left\{ \left( | z _ { 1 } | ^ { 2 } - \frac { 1 } { 2 } \right) ^ { 2 } \right. }, & { \left. \left( | z _ { 2 } | ^ { 2 } - \frac { 1 } { 2 } \right) ^ { 2 } \right\} } \\ { \text { elsewhere on } D, } \end{array} \right. \end{equation*}
satisfies $M u = 0$ on $D$, $u| _ { \partial D } = f$.
However, if $f$ and $\phi$ are both smooth and $\phi > 0$ on $D$, then was shown in [a8] that there exists a smooth $u$ satisfying (a1).
There have been defined several capacity functions (cf. also Capacity; Capacity potential) on $\mathbf{C} ^ { n }$ that all share the property that sets of capacity $0$ are precisely the pluripolar sets, i.e. sets that are locally contained in the $- \infty$ locus of plurisubharmonic functions. See [a4], [a10], [a23], [a24]. Firstly, the classical construction of logarithmic capacity carries over: Let
\begin{equation*} \mathcal{L} = \{ u \in \operatorname { PSH } ( \mathbf{C} ^ { n } ) : u - \operatorname { log } ( 1 + | z | ) = O ( 1 ) ( z \rightarrow \infty ) \}. \end{equation*}
For a bounded set $E$ in $\mathbf{C} ^ { n }$, define the Green function with pole at infinity by
\begin{equation*} L _ { E } ( z ) = \operatorname { sup } \{ v ( z ) : v \in \mathcal{L} , v \leq 0 \text { on } E \}. \end{equation*}
Set $L _ { E } ^ { * } ( z ) = \operatorname { limsup } _ { w \rightarrow z } L _ { E } ( w )$, the upper semi-continuous regularization of $L_{E}$. Then either $L _ { E } ^ { * } \equiv \infty$ or $L \in \operatorname { PSH } ( \mathbf{C} ^ { n } )$. For $u \in \mathcal{L}$ one defines the Robin function on $\mathbf{C} ^ { n }$ by
\begin{equation*} \rho _ { u } ( z ) = \limsup _ { t \in \text{C} } ( u ( t z ) - \operatorname { log } | t z | ). \end{equation*}
Next the logarithmic capacity of $E$ is defined as
\begin{equation*} \operatorname { Cap } ( E ) = \operatorname { exp } \left( - \operatorname { sup } _ { z \in \text{C} ^ { n } } \rho _ { L _ { E } } ( z ) \right). \end{equation*}
It is, however, a non-trivial result that 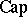 is a Choquet capacity (cf. Capacity), see [a17]. Another important (relative) capacity is the Monge–Ampère capacity introduced by Bedford and Taylor, [a4]. It is defined as follows: Let $\Omega$ be a strictly pseudo-convex domain in $\mathbf{C} ^ { n }$ and let $K$ be a compact subset of $\Omega$. The Monge–Ampère capacity of $K$ relative to $\Omega$ is
is a Choquet capacity (cf. Capacity), see [a17]. Another important (relative) capacity is the Monge–Ampère capacity introduced by Bedford and Taylor, [a4]. It is defined as follows: Let $\Omega$ be a strictly pseudo-convex domain in $\mathbf{C} ^ { n }$ and let $K$ be a compact subset of $\Omega$. The Monge–Ampère capacity of $K$ relative to $\Omega$ is
\begin{equation*} C ( K , \Omega ) = \end{equation*}
\begin{equation*} = \operatorname { sup } \left\{ \int _ { K } M ( u ) d V : u \in \operatorname { PSH } ( \Omega ) , 0 < u < 1 \right\}. \end{equation*}
If $E \subset \Omega$ is an arbitrary subset, one defines
\begin{equation*} C ( E , \Omega ) = \operatorname { sup } \{ C ( K ) : K \subset \Omega \}. \end{equation*}
It is shown in [a4] that plurisubharmonic functions are quasi-continuous, i.e. continuous outside an open set of arbitrarily small capacity. Another application is a new proof of the following Josefson theorem [a14]: If $E \subset \mathbf{C} ^ { n }$ is pluripolar, then there exists a $u \in \operatorname { PSH } ( \mathbf{C} ^ { n } )$ with $u | _ { E } = - \infty$.
Although there is no analogue of the Riesz decomposition theorem (cf. also Riesz theorem; Riesz decomposition theorem), there are notions of Green functions.
1) The (Klimek or pluricomplex) Green function on a domain $\Omega \subset {\bf C} ^ { n }$ with pole at $w \in \Omega$ is the function
\begin{equation*} G ( z , w ) = \end{equation*}
\begin{equation*} = \operatorname { sup } \left\{ h ( z ) : \begin{array}{ c c } { h \in \operatorname{PSH}(\Omega), \, h<0,} \\{h ( \zeta ) - \operatorname { log } \| \zeta - w \| = O ( 1 ) ( \zeta \rightarrow w )} \end{array} \right\}. \end{equation*}
If $\Omega$ is hyperconvex, i.e. pseudo-convex and admitting a bounded plurisubharmonic exhaustion function, then $G ( z , w )$ is negative and, for $w$ fixed, tends to $0$ if $z \rightarrow \partial \Omega$. Moreover, $M ( G ( z , w ) ) = ( 2 \pi ) ^ { n } \delta _ { w }$, where $\delta _ { W }$ is the Dirac distribution at $w$; see [a12], [a15] for more details.
2) The symmetric Green function on a domain $\Omega \subset {\bf C} ^ { n }$ is the function
\begin{equation*} W ( z , w ) = \operatorname { sup } h ( z , w ) \end{equation*}
where the supremum is taken over
\begin{equation*} h \in \operatorname { SPSH } ( \Omega \times \Omega ) , h < 0, \end{equation*}
\begin{equation*} h ( z , w ) - \operatorname { log } \| z - w \| \leq \end{equation*}
\begin{equation*} \leq - \operatorname { log } ( \operatorname { max } \{ \operatorname { dist } ( z , \partial \Omega ) , \operatorname { dist } ( w , \partial \Omega ) \} ). \end{equation*}
Here, $\operatorname { SPSH } ( \Omega \times \Omega )$ stands for the functions $f ( z , w )$ on $\Omega \times \Omega$ that are plurisubharmonic in each of the variables $z$, $w$ separately, when the other is kept fixed. On strictly pseudo-convex domains $\Omega$, the symmetric Green function is negative and, for $w$ fixed, tends to $0$ as $z \rightarrow \partial \Omega$.
In general $W \leq G$, and there need not be equality, see [a2]. In particular, $G$ need not be symmetric and $W$ need not be a fundamental solution of $M$. However, on bounded convex domains $G = W$. This is based on work of L. Lempert [a20], [a21] showing that on bounded convex domains in $\mathbf{C} ^ { n }$ the Kobayashi distance $K ( z , w )$ (cf. Hyperbolic metric), the Lempert functional $\delta ( z , w )$ and the Carathéodory distance $C ( z , w )$ (cf. also Green function) coincide. The relation between these objects and the Green functions on a domain $\Omega$ is (see e.g. [a10])
\begin{equation*} \operatorname { log } \operatorname { tanh } C ( z , w ) \leq W ( z , w ) \leq \end{equation*}
\begin{equation*} \leq G ( z , w ) \leq \operatorname { log } \operatorname { tanh } \delta ( z , w ), \end{equation*}
where $\delta$ is the Lempert functional
\begin{equation*} \delta ( z , w ) = \operatorname { inf } _ { f \in \mathcal{F} } \{ \operatorname { log } | \xi | : f ( \xi ) = z , f ( 0 ) = w \}, \end{equation*}
with $\mathcal{F}$ the family of holomorphic mappings from the unit disc in $\mathbf{C}$ to $\Omega$.
The Green function is instrumental in the following result of Z. Błocki and P. Pflug, [a6], which is one of the first applications outside pluripotential theory: Every bounded hyperconvex domain is complete in the Bergman metric (cf. Bergman spaces).
A more elementary proof is given in [a13].
References
| [a1] | E. Bedford, "Survey of pluri-potential theory" , Several Complex Variables (Stockholm, 1987/8) , Math. Notes , 38 , Princeton Univ. Press (1993) pp. 48–97 |
| [a2] | E. Bedford, J.P. Demailly, "Two counterexamples concerning the pluri-complex Green function in $\mathbf{C} ^ { n }$" Indiana Univ. Math. J. , 37 (1988) pp. 865–867 |
| [a3] | E. Bedford, B.A. Taylor, "The Dirichlet problem for a complex Monge–Ampère equation" Invent. Math. , 37 (1976) pp. 1–44 |
| [a4] | E. Bedford, B.A. Taylor, "A new capacity for plurisubharmonic functions" Acta Math. , 149 (1982) pp. 1–40 |
| [a5] | Z. Błocki, "The complex Monge–Ampère equation in hyperconvex domain" Ann. Scuola Norm. Sup. Pisa , 23 (1996) pp. 721–747 |
| [a6] | Z. Błocki, P. Pflug, "Hyperconvexity and Bergman completeness" Nagoya Math. J. , 151 (1998) pp. 221–225 |
| [a7] | H. Bremermann, "On the conjecture of equivalence of plurisubharmonic functions and Hartogs functions" Math. Ann. , 131 (1956) pp. 76–86 |
| [a8] | L. Caffarelli, J.J. Kohn, L. Nirenberg, J. Spruck, "The Dirichlet problem for nonlinear second order elliptic equations. II. Complex Monge–Ampère, and uniform elliptic, equations" Commun. Pure Appl. Math. , 38 (1985) pp. 209–252 |
| [a9] | U. Cegrell, "Discontinuité de l'opérateur de Monge Ampère complexe" C.R. Acad. Sci. Paris Sér. I Math. , 296 (1983) pp. 869–871 |
| [a10] | U. Cegrell, "Capacities in complex analysis" , Vieweg (1988) |
| [a11] | U. Cegrell, "Pluricomplex energy" Acta Math. , 180 (1998) pp. 187–217 |
| [a12] | J.P. Demailly, "Mesures de Monge–Ampère et mesures pluriharmoniques" Math. Z. , 194 (1987) pp. 519–564 |
| [a13] | G. Herbort, "The Bergman metric on hyperconvex domains" Math. Z. , 232 (1999) pp. 183–196 |
| [a14] | B. Josefson, "On the equivalence between locally polar and globally polar sets for plurisubharmonic functions on $\mathbf{C} ^ { n }$" Ark. Mat. , 16 (1978) pp. 109–115 |
| [a15] | M. Klimek, "Extremal plurisubharmonic functions and invariant pseudodistances" Bull. Soc. Math. France , 113 (1985) pp. 231–240 |
| [a16] | M. Klimek, "Pluripotential theory" , Clarendon Press/Oxford Univ. Press (1991) |
| [a17] | S. Kołodziej, "The logarithmic capacity in $\mathbf{C} ^ { n }$" Ann. Polon. Math. , 48 (1988) pp. 253–267 |
| [a18] | S. Kołodziej, "The complex Monge–Ampère equation" Acta Math. , 180 (1998) pp. 69–117 |
| [a19] | P. Lelong, "Les fonctions plurisousharmonique" Ann. Sci. École Norm. Sup. , 62 (1945) pp. 301–338 |
| [a20] | L. Lempert, "La métrique de Kobayashi et la représentation des domaines sur la boule" Bull. Soc. Math. France , 109 (1981) pp. 427–474 |
| [a21] | L. Lempert, "Holomorphic retracts and intrinsic metrics in convex domains" Anal. Math. , 8 : 4 (1982) pp. 257–261 |
| [a22] | K. Oka, "Sur les fonctions analytiques de plusieurs variables VI. Domaines pseudoconvexes" Tôhoku Math. J. , 49 (1942) pp. 15–52 |
| [a23] | A. Sadullaev, "Plurisubharmonic measures and capacities on complex manifolds" Russian Math. Surveys , 36 (1981) pp. 61–119 Uspekhi Mat. Nauk. , 36 (1981) pp. 53–105 |
| [a24] | J. Siciak, "Extremal functions and capacities in $\mathbf{C} ^ { n }$" Sophia Kokyuroku Math. , 14 (1982) |
Pluripotential theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pluripotential_theory&oldid=55418