Plancherel theorem
For any square-summable function 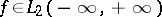 the integral
the integral
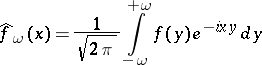 |
converges in 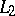 to some function
to some function 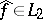 as
as  , i.e.
, i.e.
 | (1) |
Here the function 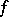 itself is representable as the limit in
itself is representable as the limit in 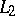 of the integrals
of the integrals
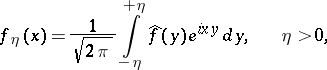 |
as 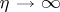 , i.e.
, i.e.
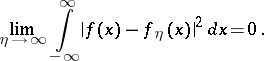 |
Also, the following relation holds:
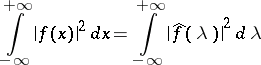 |
(the Parseval–Plancherel formula).
The function
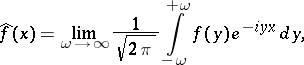 |
where the limit is understood in the sense of convergence in 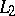 (as in (1)), is called the Fourier transform of
(as in (1)), is called the Fourier transform of 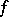 ; it is sometimes denoted by the symbolic formula:
; it is sometimes denoted by the symbolic formula:
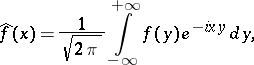 | (2) |
where the integral in (2) must be understood in the sense of the principal value at 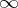 in the metric of
in the metric of  . One similarly interprets the equation
. One similarly interprets the equation
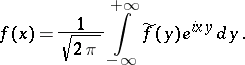 | (3) |
For functions 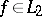 , the integrals (2) and (3) exist in the sense of the principal value for almost all
, the integrals (2) and (3) exist in the sense of the principal value for almost all  .
.
The functions 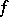 and
and 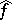 also satisfy the following equations for almost-all
also satisfy the following equations for almost-all  :
:
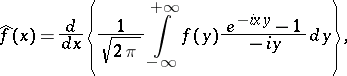 |
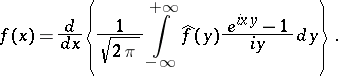 |
If Fourier transformation is denoted by  and if
and if 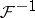 denotes the inverse, then Plancherel's theorem can be rephrased as follows:
denotes the inverse, then Plancherel's theorem can be rephrased as follows: 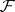 and
and 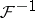 are mutually-inverse unitary operators on
are mutually-inverse unitary operators on 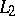 (cf. Unitary operator).
(cf. Unitary operator).
The theorem was established by M. Plancherel (1910).
References
| [1] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [2] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [3] | S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German) |
Comments
The heart of Plancherel's theorem is the assertion that if 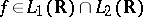 , then: a)
, then: a) 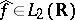 , where
, where 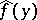 is defined by (2) for
is defined by (2) for 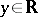 ; b)
; b) 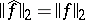 ; and c) the set of all such
; and c) the set of all such 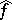 is dense in
is dense in 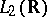 . Then one extends this mapping
. Then one extends this mapping 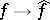 to a unitary mapping
to a unitary mapping 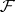 of
of 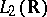 onto itself which satisfies
onto itself which satisfies 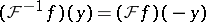 for almost every
for almost every 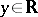 . There are generalizations of Plancherel's theorem in which
. There are generalizations of Plancherel's theorem in which 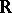 is replaced by
is replaced by 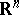 or by any locally compact Abelian group. Cf. also Harmonic analysis, abstract.
or by any locally compact Abelian group. Cf. also Harmonic analysis, abstract.
References
| [a1] | W. Rudin, "Fourier analysis on groups" , Wiley (1962) |
| [a2] | A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940) |
| [a3] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [a4] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1979) |
| [a5] | H. Reiter, "Classical harmonic analysis and locally compact groups" , Oxford Univ. Press (1968) |
Plancherel theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plancherel_theorem&oldid=16182