Pierpont variation
One of the numerical characteristics of a function of several variables which can be considered as a multi-dimensional analogue of the variation of a function of one variable. Let a function  ,
,  be given on an
be given on an  -dimensional parallelopipedon
-dimensional parallelopipedon
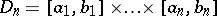 |
and let  ,
,  , be a subdivision of the segment
, be a subdivision of the segment  into
into  ,
,  equal segments by points
equal segments by points
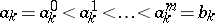 |
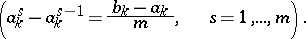 |
These subdivisions generate a subdivision
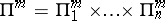 |
of the parallelopipedon 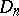 into
into 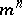 parallelopipeda
parallelopipeda 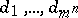 with edges parallel to the coordinate axes.
with edges parallel to the coordinate axes.
Let
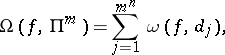 |
where 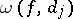 is the oscillation of the function
is the oscillation of the function 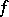 on
on 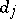 (cf. Oscillation of a function). Then
(cf. Oscillation of a function). Then
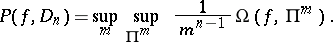 |
If  , then the function
, then the function 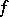 is said to be of bounded (finite) Pierpont variation on
is said to be of bounded (finite) Pierpont variation on  , and the class of all such functions is denoted by
, and the class of all such functions is denoted by  . This definition was suggested by J. Pierpont [1]. The class
. This definition was suggested by J. Pierpont [1]. The class 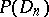 contains as a subset the class
contains as a subset the class  of all functions of bounded Arzelà variation on
of all functions of bounded Arzelà variation on 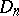 .
.
References
| [1] | J. Pierpont, "Lectures on the theory of functions of real variables" , 1 , Dover, reprint (1959) |
| [2] | H. Hahn, "Reellen Funktionen" , 1 , Chelsea, reprint (1948) |
Pierpont variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pierpont_variation&oldid=13447