Piecewise-linear topology
The branch of topology dealing with polyhedra. By a polyhedron one means, first and foremost, a subset of a topological vector space which is a finite or locally finite union of convex polytopes of bounded dimension, but also topological polyhedra with a fixed piecewise-linear structure (see below). By locally finite one means that each point in the ambient space has a neighbourhood which intersects only finitely many elements of the union. The concept of a polyhedron lies midway between the concepts of a topological space and a simplicial complex (the latter is introduced in order to permit a more constructive study first of spaces homeomorphic to polyhedra and subsequently of more general spaces). A space homeomorphic to a polyhedron is called a topological polyhedron (t-polyhedron). The class of t-polyhedra contains the most important objects of finite-dimensional topology — primarily smoothable manifolds.
With an eye to finitization of the study of polyhedra, one considers the four categories  . The objects of
. The objects of  are the t-polyhedra; its morphisms are continuous mappings. The objects of
are the t-polyhedra; its morphisms are continuous mappings. The objects of  are the polyhedra, and its morphisms are piecewise-linear mappings (pl-mappings), i.e. mappings which linearly transform the convex polytopes of some covering of the domain into polytopes of some covering of the range. The objects in
are the polyhedra, and its morphisms are piecewise-linear mappings (pl-mappings), i.e. mappings which linearly transform the convex polytopes of some covering of the domain into polytopes of some covering of the range. The objects in  are the simplicial complexes, i.e. polyhedra with a fixed regular covering by simplices (a covering such that two simplices may intersect only along a common face), the morphisms in
are the simplicial complexes, i.e. polyhedra with a fixed regular covering by simplices (a covering such that two simplices may intersect only along a common face), the morphisms in  are simplicial mappings, i.e. pl-mappings which linearly transform each simplex of the domain onto some simplex of the range. Finally,
are simplicial mappings, i.e. pl-mappings which linearly transform each simplex of the domain onto some simplex of the range. Finally,  consists of abstract complexes (a-complexes) and their simplicial mappings. An a-complex in
consists of abstract complexes (a-complexes) and their simplicial mappings. An a-complex in  is an at most countable set
is an at most countable set  with a distinguished system of finite subsets of bounded cardinality, called simplices, which satisfy the following conditions: 1) for each simplex
with a distinguished system of finite subsets of bounded cardinality, called simplices, which satisfy the following conditions: 1) for each simplex  the distinguished system also contains all subsets of the simplex — the faces of
the distinguished system also contains all subsets of the simplex — the faces of  ; and 2) each simplex is a face of at most finitely many other simplices. A mapping of sets possessing the structure of a-complexes is said to be simplicial if it takes simplices of the domain onto simplices of the range. The dimension of a simplex in an a-complex is one less than the number of its elements. Each element of the set
; and 2) each simplex is a face of at most finitely many other simplices. A mapping of sets possessing the structure of a-complexes is said to be simplicial if it takes simplices of the domain onto simplices of the range. The dimension of a simplex in an a-complex is one less than the number of its elements. Each element of the set  is a face of the complex
is a face of the complex  and is called a vertex of
and is called a vertex of 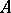 . It is convenient to assume that each a-complex contains the empty simplex, denoted by 1.
. It is convenient to assume that each a-complex contains the empty simplex, denoted by 1.
There exist forgetful functors
 |
In fact, a polyhedron defines a topological space, and a pl-mapping is continuous, this gives 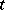 ;
; 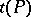 is called the space of the polyhedron
is called the space of the polyhedron 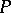 . Each complex defines a polyhedron, and a simplicial mapping of complexes is a pl-mapping, this gives
. Each complex defines a polyhedron, and a simplicial mapping of complexes is a pl-mapping, this gives 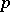 ;
; 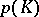 is called the body or skeleton of the complex and is denoted by
is called the body or skeleton of the complex and is denoted by 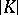 . Finally, the set of vertices of a complex
. Finally, the set of vertices of a complex 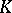 contains distinguished subsets — the sets of vertices of the simplices in
contains distinguished subsets — the sets of vertices of the simplices in 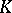 , and this defines an a-complex; a simplicial mapping of complexes defines a simplicial mapping of the corresponding a-complexes. This gives
, and this defines an a-complex; a simplicial mapping of complexes defines a simplicial mapping of the corresponding a-complexes. This gives  , and
, and  is called the scheme of the complex
is called the scheme of the complex 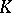 . These functors do not have natural inverses. However, they become equivalences if one goes over to suitable quotient categories. The natural isomorphisms are called, respectively, homeomorphisms in
. These functors do not have natural inverses. However, they become equivalences if one goes over to suitable quotient categories. The natural isomorphisms are called, respectively, homeomorphisms in  , pl-homeomorphisms in
, pl-homeomorphisms in  , and simplicial isomorphisms in
, and simplicial isomorphisms in 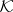 and
and 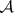 . For every a-complex
. For every a-complex  one can define a realization as follows. In a topological vector space
one can define a realization as follows. In a topological vector space 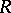 , choose a set of points
, choose a set of points 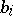 that correspond one-to-one with the vertices of
that correspond one-to-one with the vertices of 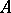 and are moreover in general position in
and are moreover in general position in  (this may be done if e.g. the dimension of
(this may be done if e.g. the dimension of  exceeds twice that of
exceeds twice that of  ), in such a way that only finitely many points lie in a bounded region of the space. Every set of points
), in such a way that only finitely many points lie in a bounded region of the space. Every set of points  corresponding to the same simplex in
corresponding to the same simplex in 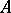 spans a certain simplex in
spans a certain simplex in 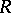 ; the union of all such simplices yields a complex with as scheme precisely
; the union of all such simplices yields a complex with as scheme precisely  — a realization of
— a realization of 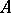 . All realizations of the same a-complex are isomorphic, so that the functor
. All realizations of the same a-complex are isomorphic, so that the functor  establishes a one-to-one correspondence between the classes of isomorphic complexes in
establishes a one-to-one correspondence between the classes of isomorphic complexes in 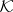 and in
and in 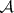 . Any polyhedron
. Any polyhedron 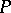 is the skeleton of some complex
is the skeleton of some complex 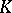 , in which case
, in which case  is known as a rectilinear triangulation of
is known as a rectilinear triangulation of 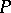 , or simply a triangulation; a scheme of
, or simply a triangulation; a scheme of 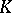 is known as an abstract triangulation of
is known as an abstract triangulation of 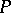 . Given a pl-mapping
. Given a pl-mapping 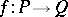 there exist triangulations
there exist triangulations 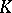 for
for 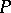 and
and  for
for  so that
so that  is a simplicial mapping of
is a simplicial mapping of 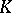 into
into 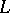 . Different triangulations of a polyhedron need not be isomorphic, so that one obtains a coarser equivalence relation in
. Different triangulations of a polyhedron need not be isomorphic, so that one obtains a coarser equivalence relation in 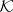 . A refinement of a complex
. A refinement of a complex 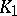 is defined as a complex
is defined as a complex 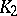 such that
such that  and such that each simplex of
and such that each simplex of  is a subset of some simplex of
is a subset of some simplex of 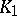 . A complex
. A complex 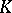 is combinatorially equivalent to
is combinatorially equivalent to  if
if 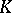 and
and 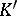 possess isomorphic refinements. Two complexes
possess isomorphic refinements. Two complexes 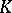 and
and 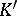 are combinatorially equivalent if and only if
are combinatorially equivalent if and only if 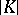 is pl-homeomorphic to
is pl-homeomorphic to  . In other words, the functor
. In other words, the functor 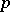 establishes a natural correspondence between the classes of combinatorially equivalent complexes and pl-homeomorphic polyhedra. The functor
establishes a natural correspondence between the classes of combinatorially equivalent complexes and pl-homeomorphic polyhedra. The functor 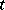 is epimorphic (by definition). A polyhedron
is epimorphic (by definition). A polyhedron 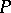 is known as a rectilinear realization of the t-polyhedron
is known as a rectilinear realization of the t-polyhedron 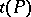 . The assertion that any two realizations of a t-polyhedron are pl-homeomorphic is known as the fundamental conjecture of combinatorial topology (the Hauptvermutung); it has been proved false [3]. It is thus meaningful to define pl-structures on t-polyhedra: A pl-structure is given by a homeomorphism
. The assertion that any two realizations of a t-polyhedron are pl-homeomorphic is known as the fundamental conjecture of combinatorial topology (the Hauptvermutung); it has been proved false [3]. It is thus meaningful to define pl-structures on t-polyhedra: A pl-structure is given by a homeomorphism 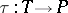 of a t-polyhedron onto a polyhedron, with two homeomorphisms
of a t-polyhedron onto a polyhedron, with two homeomorphisms 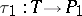 and
and 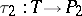 considered to define the same structure if
considered to define the same structure if 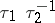 is a pl-homeomorphism;
is a pl-homeomorphism; 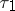 and
and 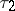 define equivalent (but not necessarily identical) structures if
define equivalent (but not necessarily identical) structures if 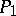 and
and 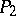 are pl-homeomorphic. A t-polyhedron with a fixed pl-structure is also called a polyhedron. Finally, the relation of combinatorial equivalence in
are pl-homeomorphic. A t-polyhedron with a fixed pl-structure is also called a polyhedron. Finally, the relation of combinatorial equivalence in 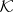 implies, via the functor
implies, via the functor  , a new equivalence relation in
, a new equivalence relation in 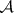 . In order to formulate this relation intrinsically in
. In order to formulate this relation intrinsically in  , it is convenient to define the operation of stellar subdivision, as follows. The join (or union) of two simplices
, it is convenient to define the operation of stellar subdivision, as follows. The join (or union) of two simplices  and
and 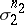 whose vertices are in general position in the vector space
whose vertices are in general position in the vector space 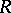 is defined as their convex hull; the latter is an
is defined as their convex hull; the latter is an  -dimensional simplex, denoted by
-dimensional simplex, denoted by 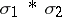 . The join of
. The join of 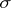 with the empty simplex 1 is
with the empty simplex 1 is 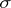 . The join of two complexes
. The join of two complexes 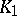 and
and 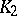 , positioned in a topological vector space
, positioned in a topological vector space 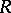 such that each simplex of
such that each simplex of 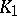 is in general position with each simplex of
is in general position with each simplex of  , is defined as the complex formed by the pairwise joins of the simplices of
, is defined as the complex formed by the pairwise joins of the simplices of 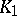 with the simplices of
with the simplices of  (it is assumed that 1 is in both
(it is assumed that 1 is in both 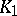 and
and  ). The star of a simplex
). The star of a simplex 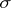 in a complex
in a complex 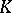 is defined as the subcomplex
is defined as the subcomplex 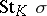 consisting of all closed simplices of which
consisting of all closed simplices of which  is a face. The star may be conceived of as the join of
is a face. The star may be conceived of as the join of 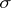 with a certain complex
with a certain complex 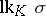 , known as the link of
, known as the link of 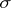 in
in 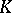 and consisting of those simplices in the star that do not intersect
and consisting of those simplices in the star that do not intersect 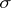 . Let
. Let  be any point in the interior of
be any point in the interior of  . In
. In 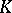 , replace all simplices of the star by simplices
, replace all simplices of the star by simplices 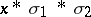 , where
, where 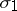 is a simplex in
is a simplex in 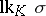 and
and 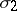 is a face of
is a face of 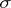 ; all other simplices of
; all other simplices of 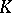 are retained. The result is a subdivision of
are retained. The result is a subdivision of 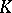 , called its subdivision with centre
, called its subdivision with centre 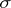 and denoted by
and denoted by 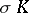 . Two complexes are combinatorially equivalent if and only if they possess isomorphic subdivisions obtained via successive stellar subdivisions and inverses of such (Alexander's theorem, [4]).
. Two complexes are combinatorially equivalent if and only if they possess isomorphic subdivisions obtained via successive stellar subdivisions and inverses of such (Alexander's theorem, [4]).
The concept of a stellar subdivision carries over to the category 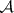 . To do this, one expresses the complexes as polynomials of a special type: The variables are the vertices of the complex, and the monomials are its simplices, including 1. Repeated simplices occurring when polynomials are added are replaced by a single monomial. Multiplication of polynomials (defined only if the factors have no common variables) is interpreted as the union of the corresponding complexes. Let
. To do this, one expresses the complexes as polynomials of a special type: The variables are the vertices of the complex, and the monomials are its simplices, including 1. Repeated simplices occurring when polynomials are added are replaced by a single monomial. Multiplication of polynomials (defined only if the factors have no common variables) is interpreted as the union of the corresponding complexes. Let 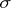 be a fixed simplex in a complex
be a fixed simplex in a complex 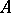 , and write
, and write 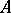 as
as 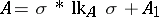 , where
, where 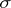 is taken out of the brackets from the union of all monomials that contain it (i.e. all monomials in
is taken out of the brackets from the union of all monomials that contain it (i.e. all monomials in 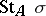 ). Inside the brackets, the link of
). Inside the brackets, the link of 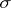 remains;
remains; 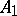 is the join of all other simplices. Replacing
is the join of all other simplices. Replacing 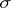 by
by 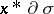 , where
, where 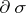 is the union of the faces of
is the union of the faces of 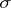 (except for
(except for 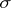 itself), including 1, one obtains a new complex
itself), including 1, one obtains a new complex 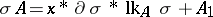 . The transformation
. The transformation 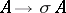 and
and 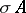 itself are known as an (abstract) stellar subdivision of
itself are known as an (abstract) stellar subdivision of 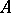 . The stellar subdivision operations in
. The stellar subdivision operations in 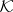 and in
and in 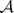 are compatible with the functor
are compatible with the functor  , so that one can represent
, so that one can represent 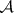 as a formal system with a countable alphabet whose constructive objects are the monomials just described and whose elementary transformations (from one object to another) are the stellar subdivisions. One can thus formulate algorithmic solvability problems in
as a formal system with a countable alphabet whose constructive objects are the monomials just described and whose elementary transformations (from one object to another) are the stellar subdivisions. One can thus formulate algorithmic solvability problems in  . For example, the problem of combinatorial equivalence of a-complexes (and consequently also of pl-homeomorphism of polyhedra) is unsolvable (Markov's theorem, [5]).
. For example, the problem of combinatorial equivalence of a-complexes (and consequently also of pl-homeomorphism of polyhedra) is unsolvable (Markov's theorem, [5]).
The original goal of the finitistic approach to complexes was to introduce invariants: An invariant is defined with respect to triangulation, and its invariance is verified only under elementary transformations (the model for this procedure was the definition of the Euler characteristic). However, this method has not achieved much popularity; firstly, owing to the invalidity of the Hauptvermutung it does not yield a proof of the topological invariance, and, secondly, the actual computation of triangulation invariants is often a hopeless task. The method has been applied, more or less systematically, in the topology of three-dimensional manifolds (cf. Topology of manifolds; Three-dimensional manifold) and in knot theory. In homotopy theory it has produced the technique of cellular decompositions (cf. CW-complex). A development of the idea of an a-complex has led to a theory of semi-simplicial complexes, which help to avoid unnecessary topological complications in homotopy theory (cf. Semi-simplicial complex).
The basic objects of piecewise-linear topology are the pl-manifolds, which serve as an important connecting link between differential and topological manifolds. The concept of a manifold can be defined naturally in each of the four categories 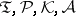 . In
. In 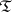 it is simply the concept of a triangulable topological manifold; in
it is simply the concept of a triangulable topological manifold; in 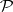 one has pl-manifolds — polyhedra each point of which has a neighbourhood that is pl-homeomorphic to a cube of suitable dimension; in
one has pl-manifolds — polyhedra each point of which has a neighbourhood that is pl-homeomorphic to a cube of suitable dimension; in 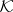 and in
and in 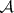 one considers combinatorial and formal manifolds, respectively — complexes (a-complexes) in which the stars of the vertices are combinatorially equivalent to the standard triangulation of a simplex, consisting of the simplex itself and all its faces. The Hauptvermutung is false in the class of pl-manifolds as well [6]. An example has been devised of a non-combinatorial triangulation of a topological manifold (see [7], [8]) in which the imbeddings of certain simplices are not locally flat. If one assumes that all simplices are locally flat and, in addition, accepts the truth of the Poincaré conjecture in dimensions 3 and 4, one can prove that a triangulation of a manifold is a combinatorial manifold. Finally, it is not known (1989) whether an arbitrary (metrizable) manifold is triangulable, though examples have been presented of manifolds with no combinatorial triangulation [6].
one considers combinatorial and formal manifolds, respectively — complexes (a-complexes) in which the stars of the vertices are combinatorially equivalent to the standard triangulation of a simplex, consisting of the simplex itself and all its faces. The Hauptvermutung is false in the class of pl-manifolds as well [6]. An example has been devised of a non-combinatorial triangulation of a topological manifold (see [7], [8]) in which the imbeddings of certain simplices are not locally flat. If one assumes that all simplices are locally flat and, in addition, accepts the truth of the Poincaré conjecture in dimensions 3 and 4, one can prove that a triangulation of a manifold is a combinatorial manifold. Finally, it is not known (1989) whether an arbitrary (metrizable) manifold is triangulable, though examples have been presented of manifolds with no combinatorial triangulation [6].
References
| [1] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
| [2] | J.R. Munkres, "Elementary differential topology" J.W. Milnor (ed.) J. Stasheff (ed.) , Characteristic classes , Princeton Univ. Press (1974) pp. 270–359 |
| [3] | J. Milnor, "Two complexes which are homeomorphic but combinatorially distinct" Ann. of Math. , 74 (1961) pp. 575–590 |
| [4] | J.W. Alexander, "Combinatorial analysis situs" Trans. Amer. Math. Soc. , 28 (1926) pp. 301–329 |
| [5] | A.A. Markov, "The unsolvability of the homeomorphism problem" Dokl. Akad. Nauk SSSR , 121 : 2 (1958) pp. 218–220 (In Russian) |
| [6] | R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" Bull. Amer. Math. Soc. , 75 (1969) pp. 742–749 |
| [7] | R.D. Edwards, "The double suspension of a certain homology 3-sphere in 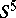 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 |
| [8] | J.W. Cannon, "Shrinking cell-like decompositions of manifolds. Codimension three" Ann. of Math. , 10 (1979) pp. 83–112 |
Comments
References
| [a1] | J.R. Stallings, "Lectures on polyhedral topology" , Tata Inst. (1967) |
| [a2] | E.C. Zeeman, "Seminar on combinatorial topology" , IHES (1963) |
| [a3] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) pp. 155–213 |
Piecewise-linear topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Piecewise-linear_topology&oldid=18956