Picard variety
of a complete smooth algebraic variety  over an algebraically closed field
over an algebraically closed field
The Abelian variety  that parametrizes the quotient group
that parametrizes the quotient group  of the group
of the group  of divisors that are algebraically equivalent to zero by the group of principal divisors
of divisors that are algebraically equivalent to zero by the group of principal divisors  , i.e. divisors of rational functions. From the point of view of the theory of sheaves, the Picard variety parametrizes the set of classes of isomorphic invertible sheaves with zero Chern class, i.e.
, i.e. divisors of rational functions. From the point of view of the theory of sheaves, the Picard variety parametrizes the set of classes of isomorphic invertible sheaves with zero Chern class, i.e.  coincides with the connected component of the unit,
coincides with the connected component of the unit,  , of the Picard group
, of the Picard group  of
of  . The structure of an Abelian variety on the group
. The structure of an Abelian variety on the group 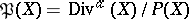 is uniquely characterized by the following property: For any algebraic family of divisors
is uniquely characterized by the following property: For any algebraic family of divisors  on
on 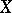 with base
with base 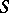 there exists a regular mapping
there exists a regular mapping 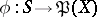 for which
for which  , where
, where 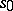 is a certain fixed point from
is a certain fixed point from  [2]. The dimension
[2]. The dimension 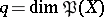 is called the irregularity of
is called the irregularity of 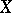 .
.
The classic example of a Picard variety is the Jacobi variety of a smooth projective curve. Another example is provided by a dual Abelian variety [3].
If  is a smooth projective complex variety,
is a smooth projective complex variety,  can be identified with the group of invertible analytic sheaves on
can be identified with the group of invertible analytic sheaves on 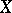 with zero Chern class [4]. Also, in that case the Picard variety
with zero Chern class [4]. Also, in that case the Picard variety  is isomorphic to the quotient group of the space
is isomorphic to the quotient group of the space 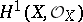 by the lattice
by the lattice 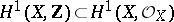 . In particular, the irregularity
. In particular, the irregularity  of
of  coincides with
coincides with  , where
, where  is the sheaf of regular
is the sheaf of regular 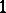 -forms. The latter result is true also in the case of non-singular projective curves over any algebraically closed field as well as in the case of complete smooth varieties over an algebraically closed field of characteristic
-forms. The latter result is true also in the case of non-singular projective curves over any algebraically closed field as well as in the case of complete smooth varieties over an algebraically closed field of characteristic  . In arbitrary characteristic one only has the Igusa inequality:
. In arbitrary characteristic one only has the Igusa inequality:  (an example is known of a smooth algebraic surface
(an example is known of a smooth algebraic surface 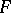 of irregularity 1 having
of irregularity 1 having 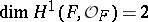 [6]). This shows that a Picard variety is closely related to the theory of one-dimensional differential forms. E. Picard himself [1] started research on such forms on Riemann surfaces; he showed that the space
[6]). This shows that a Picard variety is closely related to the theory of one-dimensional differential forms. E. Picard himself [1] started research on such forms on Riemann surfaces; he showed that the space 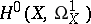 of everywhere-regular forms is finite dimensional.
of everywhere-regular forms is finite dimensional.
The concept of a Picard variety can be extended to the case of a complete normal variety 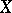 . Studies have also been made on a Picard variety
. Studies have also been made on a Picard variety  corresponding to Cartier divisors and having good functorial properties, in contrast to
corresponding to Cartier divisors and having good functorial properties, in contrast to 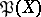 [9]. The variety
[9]. The variety 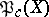 has been constructed for complete normal varieties
has been constructed for complete normal varieties 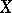 [5], as well as for arbitrary projective varieties [8].
[5], as well as for arbitrary projective varieties [8].
References
| [1] | E. Picard, "Sur les intégrales de différentielles totales algébriques" C.R. Acad. Sci. Paris , 99 (1884) pp. 961–963 |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [3] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [4] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [5] | C. Chevalley, "Sur la théorie de la variété de Picard" Amer. J. Math. , 82 (1960) pp. 435–490 |
| [6] | J.-I. Igusa, "On some problems in abstract algebraic geometry" Proc. Nat. Acad. Sci. USA , 41 : 11 (1955) pp. 964–967 |
| [7] | T. Matsusaka, "On the algebraic construction of the Picard variety I" Jap. J. Math. , 21 : 2 (1951) pp. 217–235 |
| [8] | C. Seshadri, "Variété de Picard d'une variété complète" Ann. Mat. Pura Appl. , 57 (1962) pp. 117–142 |
| [9] | C. Seshadri, "Universal property of the Picard variety of a complete variety" Math. Ann. , 158 : 3 (1965) pp. 293–296 |
Comments
The Picard variety (over an algebraically closed field) has been constructed for Weil divisors by T. Matsusaka [7], by S. Chow (see [a1]) and by A. Weil (see [a1]), and for Cartier divisors by C. Chevalley ([5], [8] and [9]).
The Jacobian of a complete (possibly singular, possibly multiple) algebraic curve was constructed by M. Rosenlicht [a2] and F. Oort [a3], [a5].
References
| [a1] | S. Lang, "Abelian varieties" , Springer (1983) |
| [a2] | M. Rosenlicht, "Generalized Jacobian varieties" Ann. of Math. , 59 (1954) pp. 505–530 |
| [a3] | F. Oort, "A construction of generalized Jacobian varieties by group extensions" Math. Ann. , 147 (1962) pp. 277–286 |
| [a4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 272 |
| [a5] | M. Flato, "Deformation view of physical theories" Czechoslovak J. Phys. , B32 (1982) pp. 472–475 |
Picard variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Picard_variety&oldid=13754