Pfaffian structure
distribution
A vector subbundle 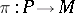 of the tangent bundle
of the tangent bundle  of a manifold
of a manifold 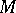 . The dimension
. The dimension 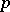 of the fibres
of the fibres 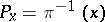 is called the dimension of the Pfaffian structure
is called the dimension of the Pfaffian structure 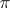 , and the number
, and the number 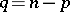 (where
(where  ) is called the rank or codimension. A Pfaffian structure of dimension
) is called the rank or codimension. A Pfaffian structure of dimension 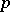 can be considered as a field of
can be considered as a field of 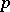 -dimensional subspaces
-dimensional subspaces 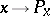 on the manifold
on the manifold 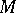 .
.
Usually a Pfaffian structure is given by a system of Pfaffian equations (cf. Pfaffian equation) 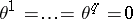 or, dually, by indicating vector fields whose values at an arbitrary point
or, dually, by indicating vector fields whose values at an arbitrary point 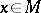 form a basis of the subspace
form a basis of the subspace 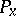 .
.
A submanifold 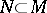 is called an integral manifold of the Pfaffian structure if
is called an integral manifold of the Pfaffian structure if 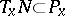 for all
for all 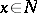 . A Pfaffian structure is said to be completely integrable if through each point
. A Pfaffian structure is said to be completely integrable if through each point 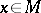 there passes a
there passes a 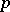 -dimensional integral manifold or, what is equivalent, if it can be locally given by a system of Pfaffian equations
-dimensional integral manifold or, what is equivalent, if it can be locally given by a system of Pfaffian equations 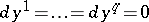 , where
, where 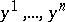 are local coordinates in
are local coordinates in 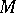 . This concept corresponds to the concept of a completely-integrable system of Pfaffian equations. Let
. This concept corresponds to the concept of a completely-integrable system of Pfaffian equations. Let 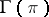 be the space of sections of the bundle
be the space of sections of the bundle 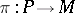 (cf. also Section of a mapping) and let
(cf. also Section of a mapping) and let 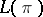 be the space of differential
be the space of differential 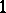 -forms (cf. Differential form) which vanish on
-forms (cf. Differential form) which vanish on 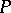 . According to Frobenius' theorem the Pfaffian structure
. According to Frobenius' theorem the Pfaffian structure 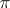 is completely integrable if and only if the space
is completely integrable if and only if the space 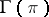 is a subalgebra of the Lie algebra
is a subalgebra of the Lie algebra 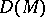 of vector fields on
of vector fields on 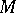 or, what is equivalent, if the ideal generated by the space
or, what is equivalent, if the ideal generated by the space 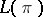 in the algebra
in the algebra 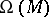 of differential forms is closed with respect to exterior differentiation.
of differential forms is closed with respect to exterior differentiation.
Let 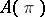 be the Lie algebra of infinitesimal automorphisms of the Pfaffian structure
be the Lie algebra of infinitesimal automorphisms of the Pfaffian structure 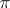 , that is, the set of vector fields
, that is, the set of vector fields 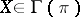 for which
for which 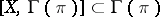 . The algebra
. The algebra 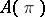 is a subalgebra of the Lie algebra
is a subalgebra of the Lie algebra 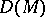 and at the same time a module over the ring
and at the same time a module over the ring 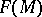 of smooth functions on
of smooth functions on 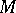 . The quotient module
. The quotient module 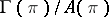 characterizes the degree of non-integrability of the Pfaffian structure.
characterizes the degree of non-integrability of the Pfaffian structure.
The Pfaffian structure 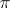 is regular if the dimension of the space
is regular if the dimension of the space 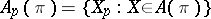 does not depend on
does not depend on 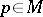 . In this case
. In this case 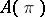 is the space of sections of a completely-integrable Pfaffian structure
is the space of sections of a completely-integrable Pfaffian structure 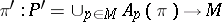 , called the characteristic system of the Pfaffian structure
, called the characteristic system of the Pfaffian structure 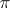 . The rank of the structure
. The rank of the structure  is called the class of the Pfaffian structure
is called the class of the Pfaffian structure 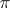 , and it is equal to the smallest possible number of coordinates of a local coordinate system in which all
, and it is equal to the smallest possible number of coordinates of a local coordinate system in which all 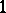 -forms in
-forms in 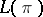 can be expressed. The class of a regular Pfaffian structure of rank 1 (that is, a field of hyperplanes) is odd and forms a complete system of local invariants: In a local coordinate system
can be expressed. The class of a regular Pfaffian structure of rank 1 (that is, a field of hyperplanes) is odd and forms a complete system of local invariants: In a local coordinate system 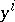 a Pfaffian structure of class
a Pfaffian structure of class 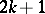 is locally given by a Pfaffian equation
is locally given by a Pfaffian equation
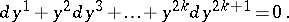 |
Another important local invariant of the Pfaffian structure is its genus, which indicates the dimension of the maximal integral non-singular manifolds (see Pfaffian problem). A complete system of local invariants of a Pfaffian structure of dimension 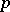 when
when 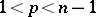 is unknown.
is unknown.
A Pfaffian structure can be considered as a 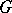 -structure of infinite type, where
-structure of infinite type, where 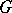 is the group of linear transformations of the space
is the group of linear transformations of the space 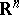 leaving invariant a
leaving invariant a 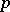 -dimensional coordinate plane. Its first-order structure function corresponds to an
-dimensional coordinate plane. Its first-order structure function corresponds to an 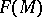 -bilinear mapping
-bilinear mapping 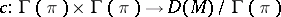 , defined by the commutation of vector fields. The space
, defined by the commutation of vector fields. The space 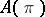 coincides with the kernel of the vector-valued bilinear form
coincides with the kernel of the vector-valued bilinear form  .
.
For references see Pfaffian problem.
Pfaffian structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pfaffian_structure&oldid=13963