Pfaffian equation
An equation of the form
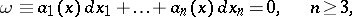 | (1) |
where 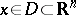 ,
, 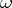 is a differential
is a differential 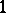 -form (cf. Differential form), and the functions
-form (cf. Differential form), and the functions 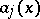 ,
,  , are real-valued. Let
, are real-valued. Let 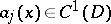 and suppose that the vector field
and suppose that the vector field  does not have critical points in the domain
does not have critical points in the domain 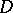 .
.
A manifold 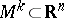 of dimension
of dimension 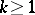 and of class
and of class 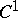 is called an integral manifold of the Pfaffian equation (1) if
is called an integral manifold of the Pfaffian equation (1) if 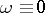 on
on 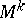 . The Pfaffian equation is said to be completely integrable if there is one and only one integral manifold of maximum possible dimension
. The Pfaffian equation is said to be completely integrable if there is one and only one integral manifold of maximum possible dimension 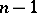 through each point of the domain
through each point of the domain 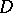 .
.
Frobenius' theorem: A necessary and sufficient condition for the Pfaffian equation (1) to be completely integrable is
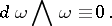 | (2) |
Here 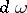 is the differential form of degree 2 obtained from
is the differential form of degree 2 obtained from 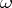 by exterior differentiation, and
by exterior differentiation, and 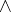 is the exterior product. In this case the integration of the Pfaffian equation reduces to the integration of a system of ordinary differential equations.
is the exterior product. In this case the integration of the Pfaffian equation reduces to the integration of a system of ordinary differential equations.
In three-dimensional Euclidean space a Pfaffian equation has the form
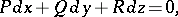 | (3) |
where 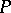 ,
, 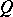 and
and 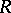 are functions of
are functions of  ,
, 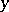 and
and  and condition (2) for complete integrability is
and condition (2) for complete integrability is
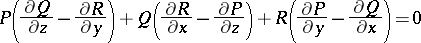 | (4) |
or
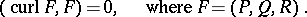 |
In this case there exist smooth functions 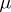 ,
, 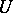 (
(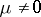 ) such that
) such that
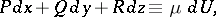 |
and the integral surfaces of the Pfaffian equation (3) are given by the equations 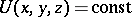 . If
. If 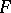 is a certain force field, then the field
is a certain force field, then the field  has
has 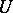 as a potential function. If the Pfaffian equation (3) is not completely integrable, then it does not have integral surfaces but can have integral curves. If arbitrary functions
as a potential function. If the Pfaffian equation (3) is not completely integrable, then it does not have integral surfaces but can have integral curves. If arbitrary functions 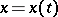 ,
, 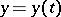 are given, then (3) will be an ordinary differential equation in
are given, then (3) will be an ordinary differential equation in  and the curve
and the curve 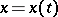 ,
, 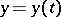 ,
, 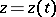 will be an integral curve.
will be an integral curve.
It was J. Pfaff [1] who posed the problem of studying equation (1) for arbitrary 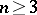 and of reducing the differential
and of reducing the differential  -form
-form  to a canonical form. Condition (4) was first obtained by L. Euler in 1755 (see [2]).
to a canonical form. Condition (4) was first obtained by L. Euler in 1755 (see [2]).
By a smooth change of variables any Pfaffian equation can locally be brought to the form
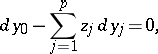 | (5) |
where 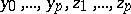 are the new independent variables (
are the new independent variables (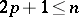 ,
, 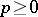 ). The number
). The number 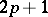 is called the class of the Pfaffian equation; here
is called the class of the Pfaffian equation; here 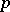 is the largest number such that the differential form
is the largest number such that the differential form 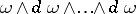 of degree
of degree 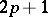 is not identically zero. When
is not identically zero. When 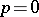 the Pfaffian equation is completely integrable. The functions
the Pfaffian equation is completely integrable. The functions 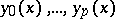 are called the first integrals of the Pfaffian equation (5) and the integral manifolds of maximum possible dimension
are called the first integrals of the Pfaffian equation (5) and the integral manifolds of maximum possible dimension 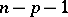 are given by the equations
are given by the equations
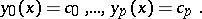 |
A Pfaffian system is a system of equations of the form
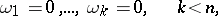 | (6) |
where 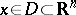 and
and  are differential
are differential 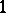 -forms:
-forms:
 |
The rank  of the matrix
of the matrix 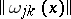 is the rank of the Pfaffian system at the point
is the rank of the Pfaffian system at the point  . A Pfaffian system is said to be completely integrable if there is one and only one integral manifold of maximum possible dimension
. A Pfaffian system is said to be completely integrable if there is one and only one integral manifold of maximum possible dimension 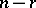 through each point
through each point 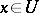 .
.
Frobenius' theorem: A necessary and sufficient condition for a Pfaffian system (6) of rank 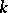 to be completely integrable is
to be completely integrable is
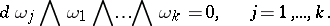 |
The problem of integrating any finite non-linear system of partial differential equations is equivalent to the problem of integrating a certain Pfaffian system (see [6]).
A number of results has been obtained on the analytic theory of Pfaffian systems. A completely-integrable Pfaffian system
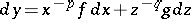 |
of 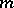 equations has been considered, where
equations has been considered, where 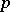 and
and 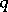 are positive integers and the vector functions
are positive integers and the vector functions 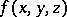 ,
, 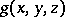 are holomorphic at the point
are holomorphic at the point 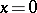 ,
, 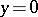 ,
, 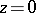 ; sufficient conditions have been given for the existence of a holomorphic solution at the origin (see [7]); generalizations to a larger number of independent variables have also been given.
; sufficient conditions have been given for the existence of a holomorphic solution at the origin (see [7]); generalizations to a larger number of independent variables have also been given.
References
| [1] | J.F. Pfaff, Berl. Abh. (1814–1815) pp. 76–135 |
| [2] | L. Euler, "Institutiones calculi differentialis" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 10 , Teubner (1980) pp. Chapt. IX ((in Latin)) |
| [3] | I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian) |
| [4] | Yu.S. Bogdanov, "Lectures on differential equations" , Minsk (1977) (In Russian) |
| [5] | E. Cartan, "Sur la théorie des systèmes en involution et ses applications à la relativité" Bull. Soc. Math. France , 59 (1931) pp. 88–118 |
| [6] | P.K. Rashevskii, "Geometric theory of partial differential equations" , Moscow-Leningrad (1947) (In Russian) |
| [7] | R. Gérard (ed.) J.-R. Ramis (ed.) , Equations différentielles et systèmes de Pfaff dans le champ complexe 1–2 , Lect. notes in math. , 712; 1015 , Springer (1979) |
Comments
The article above describes the local situation. Let 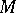 be an
be an  -dimensional manifold,
-dimensional manifold, 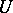 (part of) a coordinate chart. A differential
(part of) a coordinate chart. A differential 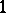 -form on
-form on  that is nowhere zero defines on the one hand a Pfaffian equation on
that is nowhere zero defines on the one hand a Pfaffian equation on 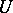 and on the other hand a one-dimensional subbundle of the cotangent bundle
and on the other hand a one-dimensional subbundle of the cotangent bundle 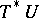 over
over 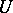 . This leads to the modern global definition of a Pfaffian equation on
. This leads to the modern global definition of a Pfaffian equation on 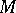 as a vector subbundle of rank 1 of
as a vector subbundle of rank 1 of 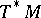 , cf. also Pfaffian structure.
, cf. also Pfaffian structure.
The statement embodied in formula (5) of the article above is known as Darboux's theorem on Pfaffian equations. There is a subtlety involved here. The Pfaffian form defining a Pfaffian equation of class 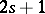 may be either of class
may be either of class 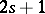 or class
or class  . Thus, Darboux's theorem (in its modern form) comes in two steps: i) let
. Thus, Darboux's theorem (in its modern form) comes in two steps: i) let 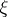 be a Pfaffian equation of constant class
be a Pfaffian equation of constant class 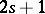 on a manifold
on a manifold 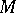 ; then everywhere locally there exists a Pfaffian form of class
; then everywhere locally there exists a Pfaffian form of class 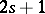 defining that equation; and ii) a canonical form statement for Pfaffian forms of class
defining that equation; and ii) a canonical form statement for Pfaffian forms of class 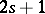 , cf. Pfaffian form.
, cf. Pfaffian form.
Here the class of a Pfaffian equation 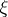 at
at 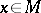 is defined by: let any differential form
is defined by: let any differential form  define
define 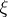 near
near  ; then the class of the equation is
; then the class of the equation is 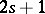 if and only if
if and only if 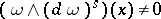 ,
, 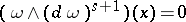 . Cf. [a1] for more details on all this.
. Cf. [a1] for more details on all this.
References
| [a1] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) pp. Chapt. V (Translated from French) |
Pfaffian equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pfaffian_equation&oldid=18964