Difference between revisions of "Peter-Weyl theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Peter–Weyl theorem to Peter-Weyl theorem: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
A theorem on the approximation of functions on a compact topological group by means of representation functions (cf. Representation function). Let 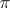 run through a family
run through a family 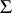 of representatives of all equivalence classes for the irreducible continuous unitary representations of a compact group
of representatives of all equivalence classes for the irreducible continuous unitary representations of a compact group 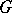 (cf. Representation of a topological group). Let
(cf. Representation of a topological group). Let 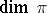 be the dimension of a representation
be the dimension of a representation 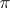 and let
and let 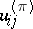 be its matrix elements in some orthonormal basis. The Peter–Weyl theorem asserts that the functions
be its matrix elements in some orthonormal basis. The Peter–Weyl theorem asserts that the functions
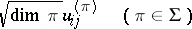 |
form an orthonormal basis in the space 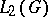 of square-summable functions with respect to the Haar measure on
of square-summable functions with respect to the Haar measure on 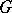 (the measure of the entire group is taken to be 1). The algebra of all complex-valued representation functions on
(the measure of the entire group is taken to be 1). The algebra of all complex-valued representation functions on 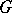 , which coincides with the set of finite linear combinations of the functions
, which coincides with the set of finite linear combinations of the functions 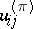 ,
, 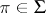 , is uniformly dense in the space of all continuous complex-valued functions in
, is uniformly dense in the space of all continuous complex-valued functions in 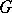 .
.
If 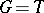 is the rotation group for the plane, this assertion coincides with an elementary theorem on approximating periodic continuous functions by trigonometric polynomials.
is the rotation group for the plane, this assertion coincides with an elementary theorem on approximating periodic continuous functions by trigonometric polynomials.
A consequence of the Peter–Weyl theorem is that the set of linear combinations of characters of the irreducible representations of 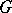 is dense in the algebra of all continuous functions on
is dense in the algebra of all continuous functions on 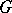 , constant on classes of conjugate elements. Another consequence is that for any element
, constant on classes of conjugate elements. Another consequence is that for any element 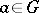 ,
, 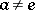 , there is an irreducible continuous representation
, there is an irreducible continuous representation 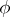 of
of 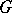 such that
such that 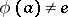 ; if, on the other hand,
; if, on the other hand, 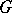 is a compact Lie group, then
is a compact Lie group, then 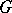 has a faithful linear representation.
has a faithful linear representation.
The Peter–Weyl theorem implies also the following more general assertion [5], [6]. Suppose one is given a continuous linear representation 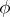 of a compact group
of a compact group 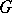 in a Fréchet space
in a Fréchet space 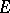 . Then the subspace of representation elements of
. Then the subspace of representation elements of 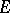 is dense in
is dense in 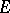 . Here an element
. Here an element 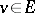 is called a representation, or spherical or almost-invariant, element if the orbit
is called a representation, or spherical or almost-invariant, element if the orbit 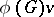 generates a finite-dimensional subspace in
generates a finite-dimensional subspace in 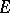 . This is applicable in particular to the case where
. This is applicable in particular to the case where 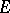 is the space of sections of a certain smoothness class of smooth vector
is the space of sections of a certain smoothness class of smooth vector 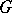 -fibrations, for example, the space of tensor fields of a certain type or given smoothness class on a smooth manifold with a smooth action of a compact Lie group
-fibrations, for example, the space of tensor fields of a certain type or given smoothness class on a smooth manifold with a smooth action of a compact Lie group 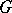 .
.
The Peter–Weyl theorem was proved in 1927 by F. Peter and H. Weyl .
References
| [1a] | F. Peter, H. Weyl, "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe" Math. Ann. , 97 (1927) pp. 737–755 |
| [1b] | F. Peter, H. Weyl, "Die Vollständigkeit der primitiven Darstellungen einer geschlossenen kontinuierlichen Gruppe" , Gesammelte Abhandlungen H. Weyl , III : 73 , Springer (1968) pp. 58–75 |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [3] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1979) |
| [4] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
| [5] | R.S. Palais, T.E. Stewart, "The cohomology of differentiable transformation groups" Amer. J. Math. , 83 : 4 (1961) pp. 623–644 |
| [6] | G.D. Mostow, "Cohomology of topological groups and solvmanifolds" Ann. of Math. , 73 : 1 (1961) pp. 20–48 |
Comments
A representation element is now usually called a 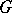 -finite element.
-finite element.
The statement that the algebra of complex-valued representation functions is uniformly dense in the algebra of continuous functions on 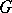 is known as the Weyl approximation theorem. The Peter–Weyl theorem gives a complete description of the (left or right) regular representation in terms of its irreducible components. In particular, each irreducible component occurs with a multiplicity equal to its dimension, cf. [a1], Chapt. 7, §2. There exists a generalized Peter–Weyl theorem for unimodular Lie groups, cf. [a1], Chapt. 14, §2. The description of
is known as the Weyl approximation theorem. The Peter–Weyl theorem gives a complete description of the (left or right) regular representation in terms of its irreducible components. In particular, each irreducible component occurs with a multiplicity equal to its dimension, cf. [a1], Chapt. 7, §2. There exists a generalized Peter–Weyl theorem for unimodular Lie groups, cf. [a1], Chapt. 14, §2. The description of 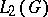 (and the other unitary representations) in terms of the irreducible representations, including the fact that the irreducible unitary representations are finite dimensional, is known as Peter–Weyl theory, cf. e.g. [a2].
(and the other unitary representations) in terms of the irreducible representations, including the fact that the irreducible unitary representations are finite dimensional, is known as Peter–Weyl theory, cf. e.g. [a2].
References
| [a1] | A.O. Barut, R. Raçzka, "Theory of group representations and applications" , 1–2 , PWN (1977) |
| [a2] | A. Wawrzyńczyk, "Group representations and special functions" , Reidel (1984) pp. Sect. 4.4 |
| [a3] | A.W. Knapp, "Representation theory of semisimple groups" , Princeton Univ. Press (1988) pp. 17 |
Peter-Weyl theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Peter-Weyl_theorem&oldid=17032