Perron-Stieltjes integral
A generalization of the Perron integral for a function of one real variable. A finite function  is said to be integrable in the sense of Perron–Stieltjes with respect to a finite function
is said to be integrable in the sense of Perron–Stieltjes with respect to a finite function  on
on  if on
if on  there exists a major function
there exists a major function  and a minor function
and a minor function  for
for  with respect to
with respect to  on
on  having
having  and such that at each point
and such that at each point 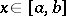 ,
,
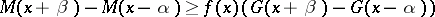 |
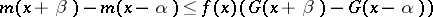 |
for all sufficiently small  and
and  , while the greatest lower bound of the numbers
, while the greatest lower bound of the numbers  , where
, where  is any such major function of
is any such major function of 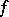 with respect to
with respect to  , and the least upper bound of the numbers
, and the least upper bound of the numbers  , where
, where  is any such minor function of
is any such minor function of  with respect to
with respect to  , coincide. Their common value is called the Perron–Stieltjes integral of
, coincide. Their common value is called the Perron–Stieltjes integral of  with respect to
with respect to  on
on 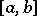 and is denoted by
and is denoted by
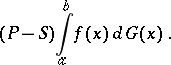 |
This generalization of the Perron integral was introduced by A.J. Ward [1].
References
| [1] | A.J. Ward, "The Perron–Stieltjes integral" Math. Z. , 41 (1936) pp. 578–604 |
| [2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [3] | I.A. Vinogradova, V.A. Skvortsov, "Generalized integrals and Fourier series" Itogi Nauk. Mat. Anal. 1970 (1971) pp. 65–107 (In Russian) |
Comments
A major function  of a function
of a function  on
on  with respect to a function
with respect to a function  on
on  is a function
is a function  such that for each
such that for each 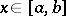 there is an
there is an 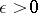 such that
such that  for all
for all 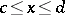 with
with 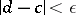 . A minor function is defined similarly, but with the inequality sign reversed. Thus, a suitable lower derivative of
. A minor function is defined similarly, but with the inequality sign reversed. Thus, a suitable lower derivative of 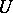 with respect to
with respect to 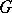 majorizes
majorizes  . More generally one considers additive interval functions
. More generally one considers additive interval functions 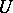 and
and 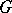 satisfying the above property, cf. [2] for details. If
satisfying the above property, cf. [2] for details. If 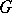 is an ordinary function on
is an ordinary function on  , then its associated additive interval function, denoted by the same letter, is
, then its associated additive interval function, denoted by the same letter, is  . A major function of
. A major function of  , without any specification of a
, without any specification of a  , is one with respect to the identify function
, is one with respect to the identify function  ,
, 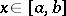 .
.
Perron-Stieltjes integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perron-Stieltjes_integral&oldid=12939