Permutator

An eigen value of a stochastic kernel that it is different from one and such that . A non-negative continuous function given on a compact set in a finite-dimensional space is called a stochastic kernel if

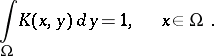The eigen values of such a kernel satisfy the condition . In operator theory, the name permutator is also given to an operator if the range of its values, , is finite dimensional and if there exists a basis in such that , .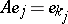

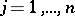References

[1]	P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian)

Comments

Given a kernel , one considers the homogeneous integral equation

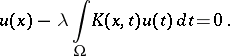A regular point of a kernel 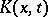is one for which this equation has only the trivial solution; a characteristic point (value) is one for which there is a non-trivial solution. If 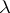is characteristic, 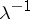is called an eigen value of the kernel 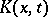. Note that it is then an eigen value of the integral operator defined by ; cf. [1], pp. 27ff.