Periodic function

A function having a period (cf. Period of a function).

Let a function be defined on and have period . To obtain the graph of it is sufficient to have the graph of on , where is a certain number, and shift it along over . If a periodic function 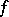with period 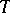has a finite derivative 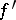, then 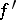is a periodic function with the same period. Let 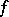be integrable over any segment and have period 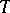. The indefinite integral 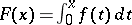has period if 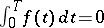, otherwise it is non-periodic, such as for example for 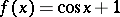, where .

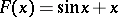A.A. Konyushkov

A periodic function of a complex variable is a single-valued analytic function 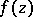having only isolated singular points (cf. Singular point) in the complex -plane and for which there exists a complex number 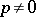, called a period of the function , such that

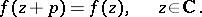Any linear combination of the periods of a given periodic function 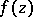with integer coefficients is also a period of 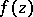. The set of all periods of a given periodic function 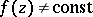constitutes a discrete Abelian group under addition, called the period group of 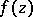. If the basis of this group consists of one unique basic, or primitive, period , i.e. if any period is an integer multiple of 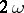, then is called a simply-periodic function. In the case of a basis consisting of two basic periods 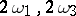, , 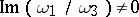one has a double-periodic function. If the periodic function is not a constant, then a basis of its period group cannot consist of more than two basic independent periods (Jacobi's theorem).

Any strip of the form

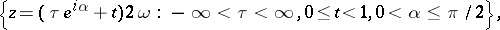where 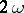is one of the basic periods of 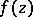or is congruent to it, is called a period strip of 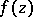; one usually takes 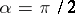, i.e. one considers a period strip with sides perpendicular to the basic period 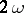. In each period strip, a periodic function takes any of its values and moreover equally often.

Any entire periodic function 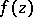can be expanded into a Fourier series throughout :

(*)

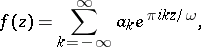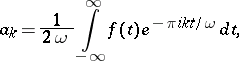which converges uniformly and absolutely on the straight line 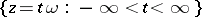and, in general, on any arbitrarily wide strip of finite width parallel to that line. The case when an entire periodic function 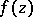tends to a certain finite or infinite limit at each of the two ends of the period strip is characterized by the fact that the series (*) contains only a finite number of terms, i.e. 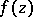should be a trigonometric polynomial.

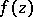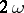Any meromorphic periodic function throughout with basic period can be represented as the quotient of two entire periodic functions with the same period, i.e. as the quotient of two series of the form (*). In particular, the class of all trigonometric functions can be described as the class of meromorphic periodic functions with period 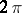that in each period strip have only a finite number of poles and tend to a definite limit at each end of the period strip.

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian)

E.D. Solomentsev

Comments

In 1), the assertion that 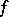has period 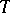means that , and 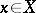implies 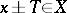and .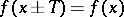

Double-periodic functions are also known as elliptic functions (cf. Elliptic function).

References

[a1]	C.L. Siegel, "Topics in complex functions" , 1 , Wiley, reprint (1988)