Period mapping
A mapping which assigns to a point  of the base
of the base 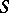 of a family
of a family 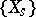 of algebraic varieties over the field
of algebraic varieties over the field 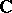 of complex numbers the cohomology spaces
of complex numbers the cohomology spaces 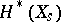 of the fibre over this point, provided with a Hodge structure. The Hodge structure thus obtained is considered as a point in the moduli variety of Hodge structures of a given type.
of the fibre over this point, provided with a Hodge structure. The Hodge structure thus obtained is considered as a point in the moduli variety of Hodge structures of a given type.
The study of period mappings dates back to the studies of N.H. Abel and C.G.J. Jacobi on integrals of algebraic functions (see Abelian differential). However, until recently, the only period mappings that have been studied were those which correspond to families of curves.
Let 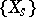 be the family of fibres
be the family of fibres 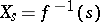 of a smooth projective morphism
of a smooth projective morphism 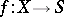 , where
, where 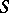 is a smooth variety. The cohomology spaces
is a smooth variety. The cohomology spaces 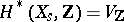 are then provided with a pure polarized Hodge structure, which is defined by a homomorphism of real algebraic groups (cf. Algebraic group)
are then provided with a pure polarized Hodge structure, which is defined by a homomorphism of real algebraic groups (cf. Algebraic group) 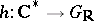 , where
, where 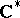 is the multiplicative group of the field of complex numbers, considered as a real algebraic group, while
is the multiplicative group of the field of complex numbers, considered as a real algebraic group, while
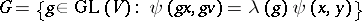 |
is the algebraic group of linear transformations of a space 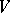 that multiply a non-singular (symmetric or skew-symmetric) bilinear form
that multiply a non-singular (symmetric or skew-symmetric) bilinear form 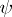 by a scalar factor; the automorphism
by a scalar factor; the automorphism 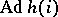 of
of 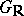 is thus a Cartan involution and
is thus a Cartan involution and 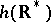 lies in the centre of
lies in the centre of  . The set
. The set 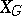 of homomorphisms
of homomorphisms 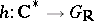 which possess the above properties is naturally provided with the
which possess the above properties is naturally provided with the  -invariant structure of a homogeneous Kähler manifold and is called a Griffiths variety, while the quotient variety
-invariant structure of a homogeneous Kähler manifold and is called a Griffiths variety, while the quotient variety 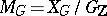 is the moduli space of the Hodge structures. The homomorphism
is the moduli space of the Hodge structures. The homomorphism 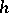 defines the Hodge decomposition
defines the Hodge decomposition
 |
of the Lie algebra 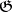 of the group
of the group 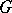 , where
, where 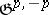 is the subspace in
is the subspace in 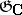 on which
on which 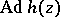 operates by multiplication by
operates by multiplication by 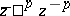 . The assignment
. The assignment 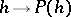 , where
, where 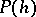 is the parabolic subgroup in
is the parabolic subgroup in 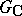 with Lie algebra
with Lie algebra 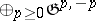 , defines an open dense imbedding of the variety
, defines an open dense imbedding of the variety 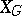 into the compact
into the compact 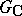 -homogeneous flag manifold
-homogeneous flag manifold 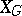 . In the tangent space
. In the tangent space
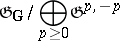 |
to 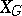 at the point
at the point 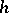 , the horizontal subspace
, the horizontal subspace
 |
is distinguished. A holomorphic mapping into 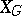 or
or 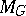 is said to be horizontal if the image of its tangential mapping lies in a horizontal subbundle.
is said to be horizontal if the image of its tangential mapping lies in a horizontal subbundle.
It has been established that the period mapping 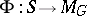 is horizontal (see , [3]). The singularities of period mappings are described by the Schmid nilpotent orbit theorem, which, when
is horizontal (see , [3]). The singularities of period mappings are described by the Schmid nilpotent orbit theorem, which, when 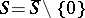 is a curve with a deleted point, asserts that if
is a curve with a deleted point, asserts that if  is the local coordinate on
is the local coordinate on 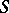 ,
, 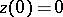 , then when
, then when 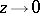 ,
, 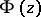 is asymptotically close to
is asymptotically close to
 |
where 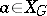 and
and 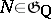 is a nilpotent element (see [4]). The image of the monodromy group
is a nilpotent element (see [4]). The image of the monodromy group
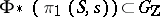 |
is semi-simple in every rational representation of the group 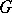 , while transference of
, while transference of 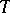 around a divisor with normal intersections
around a divisor with normal intersections 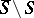 in a smooth compactification
in a smooth compactification 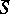 of the variety
of the variety 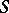 generates quasi-unipotent elements
generates quasi-unipotent elements 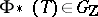 (i.e. elements which take roots of unity as eigen values). The importance of the monodromy group is underlined by the rigidity theorem (see , [2], [4]): If there are two families of algebraic varieties over
(i.e. elements which take roots of unity as eigen values). The importance of the monodromy group is underlined by the rigidity theorem (see , [2], [4]): If there are two families of algebraic varieties over  , then the relevant period mappings
, then the relevant period mappings 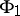 and
and 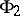 from
from 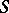 into
into 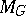 coincide if and only if
coincide if and only if 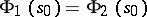 at a certain point
at a certain point 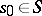 , and if the homomorphisms
, and if the homomorphisms 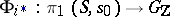 ,
, 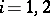 , coincide.
, coincide.
Complete results on the structure of the kernel and the image of a period mapping generally relate to the cases of curves and 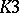 -surfaces (cf.
-surfaces (cf. 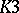 -surface). If
-surface). If  is a family of varieties of the type indicated and
is a family of varieties of the type indicated and 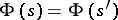 , then
, then 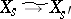 (Torelli's theorem), while for
(Torelli's theorem), while for 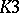 -surfaces the maximum possible image of the period mapping coincides with
-surfaces the maximum possible image of the period mapping coincides with  (see [7]). In the case of curves, the image of the period mapping has been described partially (Schottky–Yung relations, see [6], [8]). The Griffiths conjecture states that a moduli variety permits a partial analytic compactification, i.e. an open imbedding in an analytic space
(see [7]). In the case of curves, the image of the period mapping has been described partially (Schottky–Yung relations, see [6], [8]). The Griffiths conjecture states that a moduli variety permits a partial analytic compactification, i.e. an open imbedding in an analytic space 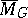 such that the period mapping
such that the period mapping 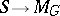 can be continued to a holomorphic mapping
can be continued to a holomorphic mapping 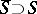 for every smooth compactification
for every smooth compactification 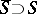 . Such a compactification is known (1983) only for the case where
. Such a compactification is known (1983) only for the case where 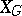 is a symmetric domain [9].
is a symmetric domain [9].
References
| [1a] | P.A. Griffiths, "Periods of integrals on algebraic manifolds I" Amer. J. of Math. , 90 (1968) pp. 568–625 |
| [1b] | P.A. Griffiths, "Periods of integrals on algebraic manifolds II" Amer. J. of Math. , 90 (1968) pp. 805–865 |
| [1c] | P.A. Griffiths, "Periods of integrals on algebraic manifolds III" Publ. Math. IHES , 38 (1970) pp. 125–180 |
| [2] | P.A. Griffiths, "A transcendental method in algebraic geometry" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 113–119 |
| [3] | P. Deligne, "Travaux de Griffiths" , Sem. Bourbaki Exp. 376 , Lect. notes in math. , 180 , Springer (1971) pp. 213–235 |
| [4] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 |
| [5] | E.H. Cattani, A.G. Kaplan, "Existence of period mappings for Hodge structures of weight two" Duke Math. J. , 4 : 1 (1977) pp. 1–43 |
| [6] | B.A. Dubrovin, "Theta-functions and non-linear equations" Russian Math. Surveys , 36 : 2 (1981) pp. 11–92 Uspekhi Mat. Nauk , 36 : 2 (1981) pp. 11–80 |
| [7] | V.A. Kulikov, Uspekhi Mat. Nauk , 32 : 4 (1977) pp. 257–258 |
| [8] | D. Mumford, Matematika , 17 : 4 (1973) pp. 34–43 |
| [9] | W. Baily, A. Borel, "Compactification of arithmetic quotients of bounded symmetric domains" Ann. of Math. , 84 (1966) pp. 442–528 |
Comments
In the one-variable case, W. Schmid also proved a very precise description of the asymptotics of the period mapping, the 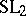 -orbit theorem. This was generalized to the several-variables case by E. Cattani and A. Kaplan [a1]. The period mapping and period domain also have been considered in the case of singularities [a1], [a2]. See also Variation of Hodge structure.
-orbit theorem. This was generalized to the several-variables case by E. Cattani and A. Kaplan [a1]. The period mapping and period domain also have been considered in the case of singularities [a1], [a2]. See also Variation of Hodge structure.
References
| [a1] | E. Cattani, A. Kaplan, "Polarized mixed Hodge structures and the local monodromy of a variation of Hodge structure" Invent. Math. , 67 (1982) pp. 101–115 |
| [a2] | E. Looijenga, "A period mapping for certain semi-universal deformations" Compos. Math. , 30 (1975) pp. 299–316 |
| [a3] | A.N. Varchenko, "Mapping of periods and intersection form" Funct. Anal. Appl. , 16 : 2 (1982) pp. 83–93 Funkts. Anal. Prilozhen. , 16 : 2 (1982) pp. 7–20 |
| [a4] | C. Peters, J.H.M. Steenbrink, "Infinitesimal variations of Hodge structures" K. Ueno (ed.) , Classical Algebraic and Analytic Manifolds , Birkhäuser (1984) pp. 399–463 |
| [a5] | P. Griffiths, "Variation of Hodge structures" P. Griffiths (ed.) , Topics in Transcendental Algebraic geometry , Princeton Univ. Press (1984) pp. 3–28 |
| [a6] | P. Griffiths, W. Schmid, "Recent developments in Hodge theory" , Discrete Subgroups of Lie Groups and Applications to Moduli , Oxford Univ. Press (1975) pp. 31–128 |
| [a7] | P. Griffiths, "Some transcendental aspects of algebraic geometry" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 3–110 |
| [a8] | J. Carlson, N.Green, P. Griffiths, J. Harris, "Infinitesimal variations of Hodge structure I" Compos. Math. , 50 (1983) pp. 109–205 |
| [a9] | R. Donagi, "Generic Torelli for hypersurfaces" Compos. Math. , 50 (1983) pp. 325–353 |
| [a10] | M. Green, "The period maps for hypersurface sections of high degree of an algebraic variety" Compos. Math. , 55 (1984) pp. 135–156 |
| [a11] | D.A. Cox, "Generic Torelli and infinitesimal variation of Hodge structure" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 , Amer. Math. Soc. (1987) pp. 235–246 |
Period mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Period_mapping&oldid=16699