Pearson product-moment correlation coefficient
While the modern theory of correlation and regression has its roots in the work of F. Galton, the version of the product-moment correlation coefficient in current use (2000) is due to K. Pearson [a2]. Pearson's product-moment correlation coefficient 
is a measure of the strength of a linear relationship between two random variables 
and 
(cf. also Random variable) with means 
, 
and finite variances 
, 
:
 |
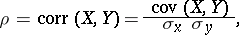where 
is the covariance of 
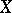and 
,
 |
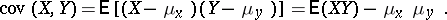It readily follows that 
, and that 
is equal to 
or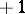 
if and only if each of 
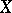and 
is almost surely a linear function of the other, i.e., 
(
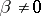) with probability 
(furthermore, 
and 
have the same sign). If 
, 
and 
are said to be uncorrelated. Independent random variables are always uncorrelated, however uncorrelated random variables need not be independent (cf. also Independence).
The term "product-moment" refers to the observation that 
, where 
denotes the 
th product moment of 
and 
about their means.
The coefficient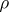 
also plays a role in linear regression (cf. also Regression analysis). If the regression of 
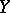on 
is linear, then 
, and if the regression of 
on 
is linear, then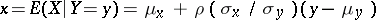 
. Note that the product of the two slopes is 
.
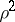When 
and 
have a bivariate normal distribution (cf. also Normal distribution), 
is a parameter of the joint density function
 |
 |
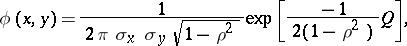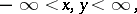with
 |
 |
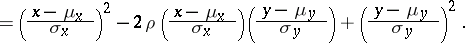Unlike the general situation, uncorrelated random variables with a bivariate normal distribution are independent.
For a random sample 
from a bivariate population,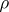 
is estimated by the sample correlation coefficient (cf. also Correlation coefficient) 
, given by
 |
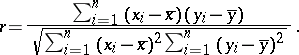If 
and 
denote, respectively, the vectors 
and 
, and 
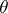denotes the angle between 
and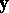 
, then
 |
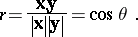Further interpretations of 
can be found in [a3]. For details on the use of 
in hypothesis testing, and for large-sample theory, see [a1].
References
| [a1] | O.J. Dunn, V.A. Clark, "Applied statistics: analysis of variance and regression" , Wiley (1974) |
| [a2] | K. Pearson, "Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia" Philos. Trans. Royal Soc. London Ser. A , 187 (1896) pp. 253–318 |
| [a3] | J.L. Rodgers, W.A. Nicewander, "Thirteen ways to look at the correlation coefficient" The Amer. Statistician , 42 (1988) pp. 59–65 |
Pearson product-moment correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pearson_product-moment_correlation_coefficient&oldid=18562