Difference between revisions of "Path-connected space"
(Importing text file) |
m (→Comments: link) |
||
| Line 11: | Line 11: | ||
====Comments==== | ====Comments==== | ||
| − | A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182027.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182028.png" /> is open and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182029.png" /> is not. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182030.png" /> defined by | + | A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point [[Sierpinski space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182027.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182028.png" /> is open and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182029.png" /> is not. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182030.png" /> defined by |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182031.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071820/p07182031.png" /></td> </tr></table> | ||
Revision as of 08:15, 3 January 2016
A topological space in which any two points can be joined by a continuous image of a simple arc; that is, a space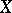 
for any two points 
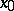and 
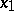of which there is a continuous mapping 
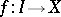of the unit interval 
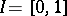such that 
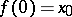and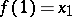 
. A path-connected Hausdorff space is a Hausdorff space in which any two points can be joined by a simple arc, or (what amounts to the same thing) a Hausdorff space into which any mapping of a zero-dimensional sphere is homotopic to a constant mapping. Every path-connected space is connected (cf. Connected space). A continuous image of a path-connected space is path-connected.
Path-connected spaces play an important role in homotopic topology. If a space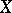 
is path-connected and 
, then the homotopy groups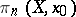 
and 
are isomorphic, and this isomorphism is uniquely determined up to the action of the group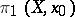 
. If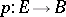 
is a fibration with path-connected base 
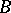, then any two fibres have the same homotopy type. If 
is a weak fibration (a Serre fibration) over a path-connected base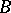 
, then any two fibres have the same weak homotopy type.
The multi-dimensional generalization of path connectedness is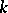 
-connectedness (connectedness in dimension 
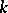). A space 
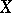is said to be connected in dimension 
if any mapping of an 
-dimensional sphere 
into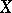 
, where 
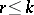, is homotopic to a constant mapping.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Comments
A connected space is not necessarily path-connected. It is not true that in an arbitrary path-connected space any two points can be joined by a simple arc: consider the two-point Sierpinski space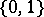 
in which 
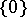is open and 
is not. The mapping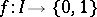 
defined by
 |
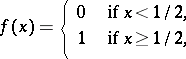is continuous and connects 0 and 1. A space in which any two points can be joined by a simple arc is called arcwise connected. Thus, path-connected Hausdorff spaces are arcwise connected.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [a2] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 15ff, 130 |
Path-connected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Path-connected_space&oldid=15741