Pascal limaçon
A plane algebraic curve of order 4; a conchoid of a circle of diameter  (see Fig.).
(see Fig.).

Figure: p071770a
The equation in rectangular coordinates is
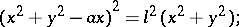 |
in polar coordinates it is
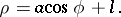 |
The coordinate origin is a double point, which is an isolated point for 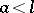 , a node for
, a node for 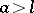 , and a cusp for
, and a cusp for  (in this case Pascal's limaçon is a cardioid). The arc length can be expressed by an elliptic integral of the second kind. The area bounded by Pascal's limaçon is
(in this case Pascal's limaçon is a cardioid). The arc length can be expressed by an elliptic integral of the second kind. The area bounded by Pascal's limaçon is
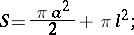 |
for 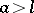 the area of the inner leaf must be counted double in calculating according to this formula. The Pascal limaçon is a special case of a Descartes oval, it is an epitrochoid (see Trochoid).
the area of the inner leaf must be counted double in calculating according to this formula. The Pascal limaçon is a special case of a Descartes oval, it is an epitrochoid (see Trochoid).
The limaçon is named after E. Pascal, who first treated it in the first half of the 17th century.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
E. Pascal is the father of B. Pascal, the famous one.
References
| [a1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a3] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) pp. 113–118 |
Pascal limaçon. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pascal_lima%C3%A7on&oldid=12704