Partial recursive operator

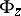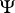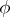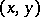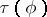A mapping from the class of all one-place functions into itself, defined as follows. Let be some enumeration operator. To this operator one naturally associates another operator , acting on one-place functions. More precisely, each function has a graph — the set of all pairs such that . Given a fixed coding method of pairs of natural numbers, this graph can be treated as a set of natural numbers. If now 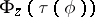is also the graph of some function 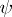, then one puts 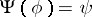. Otherwise 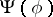is not defined. Thus, to each enumeration operator 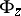one associates a partial recursive operator .

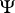If a partial recursive operator is defined on all functions, then it is called a recursive operator. A partial recursive operator that is defined on all everywhere-defined functions and that maps everywhere-defined functions to everywhere-defined functions is called a general recursive operator. Not every partial recursive operator can be extended to a recursive operator. Every general recursive operator is a recursive operator. The converse does not hold.

References

[1]	H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967)

Comments

Cf. also Recursive function; Computable function.