Partial correlation coefficient
A measure of the linear dependence of a pair of random variables from a collection of random variables in the case where the influence of the remaining variables is eliminated. More precisely, suppose that the random variables 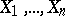 have a joint distribution in
have a joint distribution in 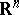 , and let
, and let 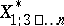 ,
, 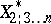 be the best linear approximations to the variables
be the best linear approximations to the variables 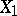 and
and 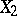 based on the variables
based on the variables 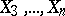 . Then the partial correlation coefficient between
. Then the partial correlation coefficient between 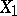 and
and 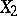 , denoted by
, denoted by 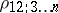 , is defined as the ordinary correlation coefficient between the random variables
, is defined as the ordinary correlation coefficient between the random variables 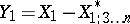 and
and 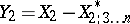 :
:
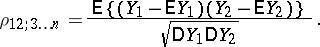 |
It follows from the definition that 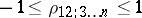 . The partial correlation coefficient can be expressed in terms of the entries of the correlation matrix. Let
. The partial correlation coefficient can be expressed in terms of the entries of the correlation matrix. Let  , where
, where 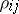 is the correlation coefficient between
is the correlation coefficient between 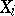 and
and 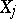 , and let
, and let 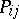 be the cofactor of the element
be the cofactor of the element 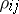 in the determinant
in the determinant 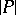 ; then
; then
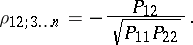 |
For example, for 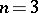 ,
,
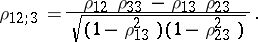 |
The partial correlation coefficient of any two variables 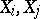 from
from 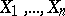 is defined analogously. In general, the partial correlation coefficient
is defined analogously. In general, the partial correlation coefficient 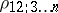 is different from the (ordinary) correlation coefficient
is different from the (ordinary) correlation coefficient 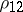 of
of 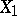 and
and 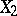 . The difference between
. The difference between 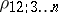 and
and 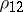 indicates whether
indicates whether 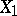 and
and 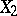 are dependent, or whether the dependence between them is a consequence of the dependence of each of them on
are dependent, or whether the dependence between them is a consequence of the dependence of each of them on 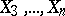 . If the variables
. If the variables 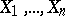 are pairwise uncorrelated, then all partial correlation coefficients are zero.
are pairwise uncorrelated, then all partial correlation coefficients are zero.
The empirical analogue of the partial correlation coefficient 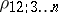 , the empirical partial correlation coefficient or sample partial correlation coefficient is the statistic
, the empirical partial correlation coefficient or sample partial correlation coefficient is the statistic
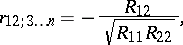 |
where 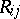 is the cofactor in the determinant of the matrix
is the cofactor in the determinant of the matrix 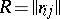 of the empirical correlation coefficients
of the empirical correlation coefficients 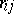 . If the results of the observations are independent and multivariate normally distributed, and
. If the results of the observations are independent and multivariate normally distributed, and 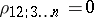 , then
, then 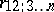 is distributed according to the probability density
is distributed according to the probability density
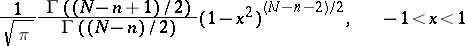 |
(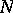 is the sample size). To test hypotheses about partial correlation coefficients, one uses the fact that the statistic
is the sample size). To test hypotheses about partial correlation coefficients, one uses the fact that the statistic
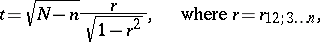 |
has, under the stated conditions, a Student distribution with 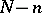 degrees of freedom.
degrees of freedom.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
Comments
References
| [a1] | R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) |
Partial correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partial_correlation_coefficient&oldid=14288