Parametric representation of univalent functions
A representation of univalent functions (cf. Univalent function) that effect a conformal mapping of planar domains onto domains of a canonical form (for example, a disc with concentric slits); it usually arises in the following manner. One chooses a one-parameter family of domains  ,
,  , included in one another,
, included in one another,  ,
,  . For
. For  one assumes known a conformal mapping
one assumes known a conformal mapping  onto some canonical domain
onto some canonical domain  . From a known mapping
. From a known mapping  of
of  onto a domain of canonical form one constructs such a mapping
onto a domain of canonical form one constructs such a mapping 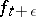 for
for  , where
, where 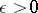 is small. Under a continuous change of the parameter
is small. Under a continuous change of the parameter 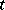 there arise in this way differential equations. The best known of these are the Löwner equation and the Löwner–Kufarev equation. In the discrete case — for lattice domains
there arise in this way differential equations. The best known of these are the Löwner equation and the Löwner–Kufarev equation. In the discrete case — for lattice domains 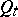 and a natural number
and a natural number 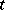 — the transition from
— the transition from 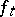 to
to 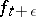 ,
,  , is effected by recurrence formulas. The source of these formulas and equations is usually the Schwarz formula (see [1]) and its generalizations (see [2]). An equally important source of parametric representations are the Hadamard variations (see [3], [4]) for the Green functions
, is effected by recurrence formulas. The source of these formulas and equations is usually the Schwarz formula (see [1]) and its generalizations (see [2]). An equally important source of parametric representations are the Hadamard variations (see [3], [4]) for the Green functions 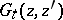 ,
, 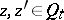 , of the family of domains mentioned above. For elliptic differential equations Hadamard's method is also called the method of invariant imbedding (see [5]). Below, the connection between parametric representations, Hadamard variations and invariant imbedding are exhibited in the simplest (discrete) case.
, of the family of domains mentioned above. For elliptic differential equations Hadamard's method is also called the method of invariant imbedding (see [5]). Below, the connection between parametric representations, Hadamard variations and invariant imbedding are exhibited in the simplest (discrete) case.
Suppose that 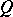 is a collection of complex integers (a lattice domain) and that the Green function
is a collection of complex integers (a lattice domain) and that the Green function 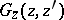 is an extremal of the Dirichlet–Douglas functional
is an extremal of the Dirichlet–Douglas functional
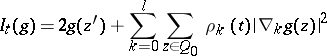 |
in the class 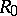 of all real-valued functions
of all real-valued functions 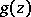 on
on 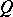 . Here
. Here 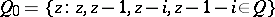 ,
,
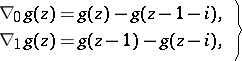 | (1) |
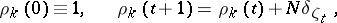 |
 is a natural number,
is a natural number, 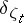 is the Kronecker symbol, and
is the Kronecker symbol, and 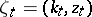 ,
, 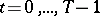 , is a certain collection of pairs of numbers;
, is a certain collection of pairs of numbers;  is the boundary of
is the boundary of 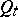 , and
, and  or 1. To find an extremum of the functional
or 1. To find an extremum of the functional 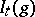 is a problem of quadratic programming. A comparison of its solutions for
is a problem of quadratic programming. A comparison of its solutions for 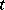 and
and 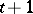 gives the basic formula of invariant imbedding (Hadamard variation):
gives the basic formula of invariant imbedding (Hadamard variation):
 | (2) |
where  and the symbol
and the symbol 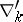 denotes the difference operators (1) in the second argument of the Green function. Knowing
denotes the difference operators (1) in the second argument of the Green function. Knowing 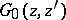 one can obtain step-by-step (recurrently) from (2) all the functions
one can obtain step-by-step (recurrently) from (2) all the functions 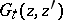 ,
, 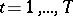 . By constructing the Green function, one obtains from the lattice analytic function
. By constructing the Green function, one obtains from the lattice analytic function 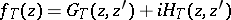 according to the equation of Cauchy–Riemann type
according to the equation of Cauchy–Riemann type
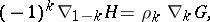 |
a univalent lattice quasi-conformal mapping 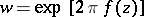 of
of  into the unit disc. Closest to the origin of coordinates is the image of
into the unit disc. Closest to the origin of coordinates is the image of  . In the limit, as
. In the limit, as 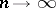 , the mapping is lattice conformal and the image of
, the mapping is lattice conformal and the image of 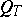 is a disc with concentric slits. The result is a continuous analogue of (2) (see [6]). When all the domains
is a disc with concentric slits. The result is a continuous analogue of (2) (see [6]). When all the domains 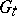 are simply connected and the canonical domain is the unit disc
are simply connected and the canonical domain is the unit disc  , one succeeds by using a fractional-linear automorphism of
, one succeeds by using a fractional-linear automorphism of 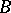 to represent the Green function in the explicit form
to represent the Green function in the explicit form
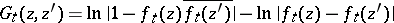 |
in terms of the function 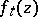 mapping
mapping  onto
onto 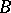 with the normalization
with the normalization 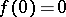 ,
, 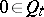 for all
for all 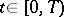 .
.
In terms of 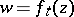 the Hadamard variation reduces to an ordinary (Löwner) differential equation. In comparison with the Hadamard variation this equation is considerably simpler; however, information on the boundary of
the Hadamard variation reduces to an ordinary (Löwner) differential equation. In comparison with the Hadamard variation this equation is considerably simpler; however, information on the boundary of 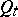 is only implicit in it — in terms of the control parameter
is only implicit in it — in terms of the control parameter 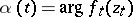 , because
, because 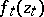 is not known beforehand. Nevertheless, the Löwner equation is a basic instrument in the parametric representation.
is not known beforehand. Nevertheless, the Löwner equation is a basic instrument in the parametric representation.
More general one-parameter families of domains 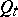 ,
, 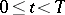 , not necessarily imbedded in one another, have also been treated (see [7]). The equations arising in such parametric representations are called Löwner–Kufarev equations. There is also a modification of the Löwner and Löwner–Kufarev equations to the case when the domains
, not necessarily imbedded in one another, have also been treated (see [7]). The equations arising in such parametric representations are called Löwner–Kufarev equations. There is also a modification of the Löwner and Löwner–Kufarev equations to the case when the domains  have a different kind of symmetry or other geometric peculiarities (see [1]).
have a different kind of symmetry or other geometric peculiarities (see [1]).
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | I.A. Aleksandrov, A.S. Sorokin, "The problem of Schwarz for multiply connected circular domains" Sib. Math. J. , 13 : 5 (1972) pp. 671–692 Sibirsk. Mat. Zh. , 13 : 5 (1972) pp. 971–1000 |
| [3] | J. Hadamard, "Mémoire sur le problème d'analyse relatif à l'équilibre des plaques élastiques encastrées" , Oeuvres , 2 , CNRS (1968) pp. 515–642 |
| [4] | J. Hadamard, "Leçons sur le calcul des variations" , 1 , Hermann (1910) |
| [5] | R. Bellma, E. Angel, "Dynamic programming and partial differential equations" , Acad. Press (1972) |
| [6] | V.I. Popov, "Quantization of control systems" Soviet Math. Dokl. , 13 : 6 (1972) pp. 1668–1672 Dokl. Akad. Nauk. SSSR , 207 : 5 (1972) pp. 1048–1050 |
| [7] | P.P. Kufarev, "On one-parameter families of analytic functions" Mat. Sb. , 13 : 1 (1943) pp. 87–118 (In Russian) (English abstract) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Parametric representation of univalent functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parametric_representation_of_univalent_functions&oldid=18588