Parallel displacement(2)
An isomorphism of fibres over the end-points 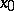 and
and 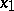 of a piecewise-smooth curve
of a piecewise-smooth curve 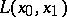 in the base
in the base 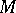 of a smooth fibre space
of a smooth fibre space 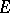 defined by some connection given in
defined by some connection given in 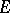 ; in particular, a linear isomorphism between the tangent spaces
; in particular, a linear isomorphism between the tangent spaces 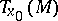 and
and 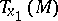 defined along a curve
defined along a curve 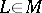 of some affine connection given on
of some affine connection given on 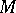 . The development of the concept of a parallel displacement began with the ordinary parallelism on the Euclidean plane
. The development of the concept of a parallel displacement began with the ordinary parallelism on the Euclidean plane 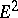 , for which F. Minding (1837) indicated a way of generalizing it to the case of a surface
, for which F. Minding (1837) indicated a way of generalizing it to the case of a surface 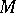 in
in 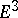 by means of the development of a curve
by means of the development of a curve 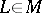 onto the plane
onto the plane 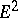 , a notion he introduced. This served as the starting point for T. Levi-Civita [1], who, by forming analytically a parallel displacement of the tangent vector to a surface, discovered that it depends only on the metric of the surface and on this basis generalized it at once to the case of an
, a notion he introduced. This served as the starting point for T. Levi-Civita [1], who, by forming analytically a parallel displacement of the tangent vector to a surface, discovered that it depends only on the metric of the surface and on this basis generalized it at once to the case of an  -dimensional Riemannian space (see Levi-Civita connection). H. Weyl [2] placed the concept of parallel displacement of a tangent vector at the base of the definition of an affine connection on a smooth manifold
-dimensional Riemannian space (see Levi-Civita connection). H. Weyl [2] placed the concept of parallel displacement of a tangent vector at the base of the definition of an affine connection on a smooth manifold 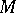 . Further generalizations of the concept are linked with the development of a general theory of connections.
. Further generalizations of the concept are linked with the development of a general theory of connections.
Suppose that on a smooth manifold 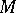 an affine connection is given by means of the matrix of local connection forms:
an affine connection is given by means of the matrix of local connection forms:
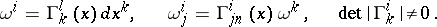 |
One says that a vector 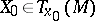 is obtained by parallel displacement from a vector
is obtained by parallel displacement from a vector 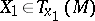 along a smooth curve
along a smooth curve 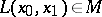 if on
if on 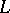 there is a smooth vector field
there is a smooth vector field 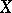 joining
joining 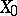 and
and 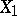 and such that
and such that 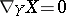 . Here
. Here 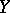 is the field of the tangent vector of
is the field of the tangent vector of 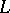 and
and 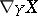 is the covariant derivative of
is the covariant derivative of 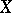 relative to
relative to 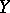 , which is defined by the formula
, which is defined by the formula
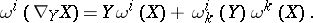 |
Thus, the coordinates 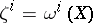 of
of 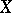 must satisfy along
must satisfy along 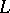 the system of differential equations
the system of differential equations
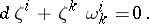 |
From the linearity of this system it follows that a parallel displacement along 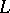 determines a certain isomorphism between
determines a certain isomorphism between 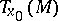 and
and 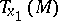 . A parallel displacement along a piecewise-smooth curve is defined as the composition of the parallel displacements along its smooth pieces.
. A parallel displacement along a piecewise-smooth curve is defined as the composition of the parallel displacements along its smooth pieces.
The automorphisms of the space 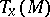 defined by parallel displacements along closed piecewise-smooth curves
defined by parallel displacements along closed piecewise-smooth curves 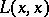 form the linear holonomy group
form the linear holonomy group 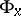 ; here
; here 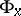 and
and 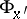 are always conjugate to each other. If
are always conjugate to each other. If 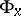 is discrete, that is, if its component of the identity is a singleton, then one talks of an affine connection with a (local) absolute parallelism of vectors, or of a (locally) flat connection. Then the parallel displacement for any
is discrete, that is, if its component of the identity is a singleton, then one talks of an affine connection with a (local) absolute parallelism of vectors, or of a (locally) flat connection. Then the parallel displacement for any 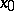 and
and 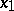 does not depend on the choice of
does not depend on the choice of 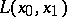 from one homotopy class; for this it is necessary and sufficient that the curvature tensor of the connection vanishes.
from one homotopy class; for this it is necessary and sufficient that the curvature tensor of the connection vanishes.
On the basis of the parallel displacement of a vector one defines the parallel displacement of a covector and, more generally, of a tensor. One says that the field of a covector 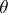 on
on 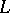 accomplishes a parallel displacement if for any vector field
accomplishes a parallel displacement if for any vector field 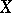 on
on 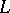 accomplishing the parallel displacement the function
accomplishing the parallel displacement the function 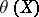 is constant along
is constant along 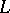 . More generally, one says that a tensor field
. More generally, one says that a tensor field 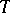 of type
of type 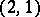 , say, accomplishes a parallel displacement along
, say, accomplishes a parallel displacement along 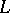 if for any
if for any 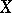 ,
, 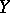 and
and 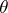 accomplishing a parallel displacement the function
accomplishing a parallel displacement the function 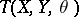 is constant along
is constant along 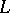 . For this it is necessary and sufficient that the components
. For this it is necessary and sufficient that the components 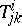 satisfy along
satisfy along 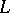 the system of differential equations
the system of differential equations
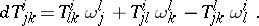 |
After E. Cartan introduced in the 1920's [3] a space of projective or conformal connection and the general concept of a connection on a manifold, the notion of parallel displacement obtained a more general content. In its most general meaning it is considered nowadays as the analysis of connections in principal fibre spaces or fibre spaces associated to them. There is a way of defining the very concept of a connection by means of that of parallel displacement, which is then defined axiomatically. However, a connection can be given by a horizontal distribution or some other equivalent manner, for example, a connection form. Then for every curve 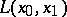 in the base
in the base 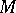 its horizontal liftings are defined as integral curves of the horizontal distribution over
its horizontal liftings are defined as integral curves of the horizontal distribution over  . A parallel displacement is then the name for a mapping that puts the end-points of these liftings in the fibre over
. A parallel displacement is then the name for a mapping that puts the end-points of these liftings in the fibre over 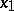 into correspondence with their other end-points in the fibre over
into correspondence with their other end-points in the fibre over 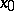 . The concepts of the holonomy group and of a (locally) flat connection are defined similarly; the latter are also characterized by the vanishing of the curvature form.
. The concepts of the holonomy group and of a (locally) flat connection are defined similarly; the latter are also characterized by the vanishing of the curvature form.
References
| [1] | T. Levi-Civita, "Nozione di parallelismo in una varietá qualunque e consequente specificazione geometrica della curvatura riemanniana" Rend. Circ. Mat. Padova , 42 (1917) pp. 173–205 |
| [2] | H. Weyl, "Raum, Zeit, Materie" , Springer (1923) |
| [3] | E. Cartan, "Les groupes d'holonomie des espaces généralisés" Acta Math. , 48 (1926) pp. 1–42 |
| [4] | K. Nomizu, "Lie groups and differential geometry" , Math. Soc. Japan (1956) |
| [5] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) pp. Chapt. II |
| [a2] | A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French) |
Parallel displacement(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_displacement(2)&oldid=16862