Paraconsistent logic
A relation of logical consequence, 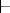 , on a set of sentences,
, on a set of sentences, 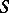 , is explosive if and only if for all
, is explosive if and only if for all 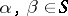 ,
,
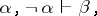 |
where "¬" is negation. A relation, and the logic that possesses it, is paraconsistent if and only if it is not explosive. Whether or not a correct consequence relation is explosive has been a contentious issue historically, but the standard formal logics of the 20th century, such as classical logic (cf. Logical calculus) and intuitionistic logic are explosive. Formal paraconsistent logics were developed by a number of different people, often working in isolation from each other, starting around the 1960s.
There are many different paraconsistent logics, with their own proof theories and model theories. Their distinctive features occur at the propositional level, though they all have full first- (and second-) order versions. In most of them validity can be defined in terms of preservation of truth in an interpretation.
In one approach, due to S. Jaśkowski, an interpretation is a Kripke model (cf. Kripke models) for some modal logic, and a sentence is true in it if it holds at some world of the interpretation. A major feature of this approach is that the inference of adjunction (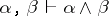 ) fails. In another, an interpretation
) fails. In another, an interpretation  ,{} is a mapping from
,{} is a mapping from 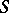 to
to 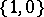 , satisfying the usual classical conditions for
, satisfying the usual classical conditions for 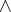 ,
, 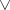 , and
, and  .
. 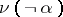 is independent of
is independent of 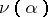 . The addition of further constraints on
. The addition of further constraints on  , such as:
, such as: 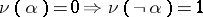 , give logics in N. da Costa's
, give logics in N. da Costa's 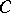 family. A feature of this approach is that it preserves all of positive logic. In a third approach, an interpretation
family. A feature of this approach is that it preserves all of positive logic. In a third approach, an interpretation  is a mapping from
is a mapping from 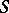 to the closed sets of a topological space
to the closed sets of a topological space 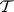 satisfying the conditions
satisfying the conditions 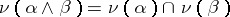 ,
, 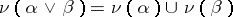 ,
, 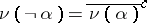 (where
(where  is the closure operator of
is the closure operator of 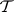 ).
). 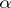 is true under
is true under  if and only if
if and only if 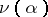 is the whole space. This gives a logic dual to intuitionistic logic.
is the whole space. This gives a logic dual to intuitionistic logic.
In a fourth approach, an interpretation is a relation 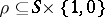 , satisfying the natural conditions
, satisfying the natural conditions
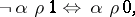 |
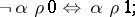 |
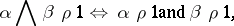 |
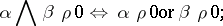 |
and dually for 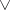 .
.  is true under
is true under 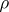 if and only if
if and only if  . This gives the logic of first degree entailment (FDE) of A. Anderson and N. Belnap. If one restricts interpretations to those satisfying the condition
. This gives the logic of first degree entailment (FDE) of A. Anderson and N. Belnap. If one restricts interpretations to those satisfying the condition 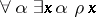 , one gets G. Priest's LP. A feature of this logic is that its logical truths coincide with those of classical logic. Thus, the law of non-contradiction holds:
, one gets G. Priest's LP. A feature of this logic is that its logical truths coincide with those of classical logic. Thus, the law of non-contradiction holds: 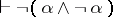 . A De Morgan lattice is a distributive lattice with an additional operator
. A De Morgan lattice is a distributive lattice with an additional operator  satisfying:
satisfying: 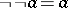 and
and 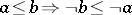 . An FDE-interpretation can be thought of as a homomorphism into the De Morgan lattice with values
. An FDE-interpretation can be thought of as a homomorphism into the De Morgan lattice with values 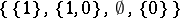 . More generally,
. More generally, 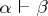 in FDE if and only if for every homomorphism
in FDE if and only if for every homomorphism 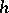 into a De Morgan lattice,
into a De Morgan lattice, 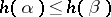 . Augmenting such lattices with an operator
. Augmenting such lattices with an operator  satisfying certain conditions, and defining validity in the same way, gives a family of relevant logics.
satisfying certain conditions, and defining validity in the same way, gives a family of relevant logics.
A paraconsistent logic localizes contradictions, and so is appropriate for reasoning from information that may be inconsistent, e.g., information stored in a computer database. It also permits the existence of theories (sets of sentences closed under deducibility) that are inconsistent but not trivial (i.e., containing everything) and of their models, inconsistent structures.
One important example of an inconsistent theory is set theory based on the general comprehension schema (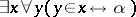 , where
, where 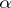 is any formula not containing
is any formula not containing  ), together with extensionality (
), together with extensionality (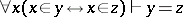 ). Another is a theory of truth (or of other semantic notions), based on the
). Another is a theory of truth (or of other semantic notions), based on the 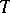 -schema (
-schema ( , where
, where  is any closed formula, and
is any closed formula, and  indicates a name-forming device), together with some mechanism for self-reference, such as arithmetization. Such theories are inconsistent due to the paradoxes of self-reference (cf. Antinomy).
indicates a name-forming device), together with some mechanism for self-reference, such as arithmetization. Such theories are inconsistent due to the paradoxes of self-reference (cf. Antinomy).
Not all paraconsistent logics are suitable as the underlying logics of these theories. In particular, if the underlying logic contains contraction (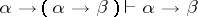 ) and modus ponens (
) and modus ponens (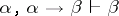 ), these theories are trivial. However, the theories are non-trivial if
), these theories are trivial. However, the theories are non-trivial if  is interpreted as the material conditional and the logic LP is used, or if it is interpreted as the conditional of some relevant logics. In the truth theories, the inconsistencies do not spread into the arithmetical machinery.
is interpreted as the material conditional and the logic LP is used, or if it is interpreted as the conditional of some relevant logics. In the truth theories, the inconsistencies do not spread into the arithmetical machinery.
Given a topos, logical operators can be defined as functors within it, and a notion of internal validity can be defined, giving intuitionistic logic. If these operators, and in particular, negation, are defined in the dual way, the internal logic of the topos is the dual intuitionistic logic. Topoi can therefore be seen as inconsistent structures.
For another example of inconsistent structures, let 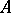 be the set of sentences true in the standard model of arithmetic. If
be the set of sentences true in the standard model of arithmetic. If 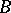 is a set of sentences in the same language properly containing
is a set of sentences in the same language properly containing 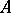 , then
, then  is inconsistent, and so has no classical models; but
is inconsistent, and so has no classical models; but  has models, including finite models, in the paraconsistent logic LP. Inconsistent (sets of) equations may have solutions in such models. The LP-models of
has models, including finite models, in the paraconsistent logic LP. Inconsistent (sets of) equations may have solutions in such models. The LP-models of  include the classical non-standard models of arithmetic (cf. Peano axioms) as a special case, and, like them, have a notable common structure.
include the classical non-standard models of arithmetic (cf. Peano axioms) as a special case, and, like them, have a notable common structure.
In inconsistent theories of arithmetic, the incompleteness theorems of K. Gödel (cf. Gödel incompleteness theorem) fail: such a theory may be axiomatizable and contain its own "undecidable" sentence (and its negation).
Inconsistent theories may be interesting or useful even if they are not true. The view that some inconsistent theories are true is called dialetheism (or dialethism).
For a general overview of the area, see [a2]. [a3] is a collection of articles, with much background material. On inconsistent mathematical structures, see [a1].
References
| [a1] | C. Mortensen, "Inconsistent mathematics" , Kluwer Acad. Publ. (1995) |
| [a2] | G. Priest, "Paraconsistent logic" D. Gabbay (ed.) F. Guenthner (ed.) , Handbook of Philosophical Logic , VII , Kluwer Acad. Publ. (to appear) (Edition: Second) |
| [a3] | "Paraconsistent logic: essays on the inconsistent" G. Priest (ed.) R. Routley (ed.) G. Norman (ed.) , Philosophia Verlag (1989) |
Paraconsistent logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Paraconsistent_logic&oldid=17427