Parabolic subgroup
A parabolic subgroup of a linear algebraic group 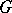 defined over a field
defined over a field 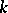 is a subgroup
is a subgroup  , closed in the Zariski topology, for which the quotient space
, closed in the Zariski topology, for which the quotient space 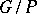 is a projective algebraic variety. A subgroup
is a projective algebraic variety. A subgroup 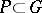 is a parabolic subgroup if and only if it contains some Borel subgroup of the group
is a parabolic subgroup if and only if it contains some Borel subgroup of the group 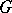 . A parabolic subgroup of the group
. A parabolic subgroup of the group 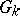 of
of  -rational points of the group
-rational points of the group 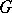 is a subgroup
is a subgroup 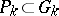 that is the group of
that is the group of  -rational points of some parabolic subgroup
-rational points of some parabolic subgroup 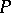 in
in 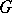 and which is dense in
and which is dense in 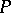 in the Zariski topology. If
in the Zariski topology. If 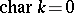 and
and 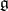 is the Lie algebra of
is the Lie algebra of 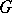 , then a closed subgroup
, then a closed subgroup 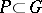 is a parabolic subgroup if and only if its Lie algebra is a parabolic subalgebra of
is a parabolic subgroup if and only if its Lie algebra is a parabolic subalgebra of 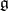 .
.
Let 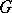 be a connected reductive linear algebraic group, defined over the (arbitrary) ground field
be a connected reductive linear algebraic group, defined over the (arbitrary) ground field 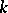 . A
. A  -subgroup of
-subgroup of 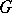 is a closed subgroup which is defined over
is a closed subgroup which is defined over 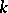 . Minimal parabolic
. Minimal parabolic 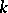 -subgroups play in the theory over
-subgroups play in the theory over  the same role as Borel subgroups play for an algebraically closed field (see ). In particular, two arbitrary minimal parabolic
the same role as Borel subgroups play for an algebraically closed field (see ). In particular, two arbitrary minimal parabolic 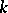 -subgroups of
-subgroups of  are conjugate over
are conjugate over 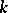 . If two parabolic
. If two parabolic  -subgroups of
-subgroups of 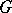 are conjugate over some extension of the field
are conjugate over some extension of the field 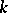 , then they are conjugate over
, then they are conjugate over 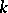 . The set of conjugacy classes of parabolic subgroups (respectively, the set of conjugacy classes of parabolic
. The set of conjugacy classes of parabolic subgroups (respectively, the set of conjugacy classes of parabolic 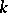 -subgroups) of
-subgroups) of 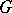 has
has 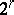 (respectively,
(respectively, 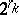 ) elements, where
) elements, where  is the rank of the commutator subgroup
is the rank of the commutator subgroup 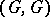 of the group
of the group 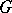 , and
, and 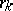 is its
is its  -rank, i.e. the dimension of a maximal torus in
-rank, i.e. the dimension of a maximal torus in  that splits over
that splits over 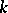 . More precisely, each such class is defined by a subset of the set of simple roots (respectively, simple
. More precisely, each such class is defined by a subset of the set of simple roots (respectively, simple 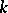 -roots) of the group
-roots) of the group 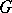 in an analogous way to that in which each parabolic subalgebra of a reductive Lie algebra is conjugate to one of the standard subalgebras (see , ).
in an analogous way to that in which each parabolic subalgebra of a reductive Lie algebra is conjugate to one of the standard subalgebras (see , ).
Each parabolic subgroup 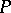 of a group
of a group 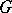 is connected, coincides with its normalizer and admits a Levi decomposition, i.e. it can be represented in the form of the semi-direct product of its unipotent radical and a
is connected, coincides with its normalizer and admits a Levi decomposition, i.e. it can be represented in the form of the semi-direct product of its unipotent radical and a 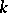 -closed reductive subgroup, called a Levi subgroup of the group
-closed reductive subgroup, called a Levi subgroup of the group 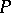 . Any two Levi subgroups in a parabolic subgroup
. Any two Levi subgroups in a parabolic subgroup 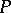 are conjugate by means of an element of
are conjugate by means of an element of  that is rational over
that is rational over  . Two parabolic subgroups of a group
. Two parabolic subgroups of a group 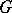 are called opposite if their intersection is a Levi subgroup of each of them. A closed subgroup of a group
are called opposite if their intersection is a Levi subgroup of each of them. A closed subgroup of a group  is a parabolic subgroup if and only if it coincides with the normalizer of its unipotent radical. Each maximal closed subgroup of a group
is a parabolic subgroup if and only if it coincides with the normalizer of its unipotent radical. Each maximal closed subgroup of a group 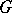 is either a parabolic subgroup or has a reductive connected component of the unit (see , ).
is either a parabolic subgroup or has a reductive connected component of the unit (see , ).
The parabolic subgroups of the group 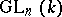 of non-singular linear transformations of an
of non-singular linear transformations of an  -dimensional vector space
-dimensional vector space 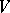 over a field
over a field 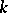 are precisely the subgroups
are precisely the subgroups 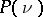 consisting of all automorphisms of the space
consisting of all automorphisms of the space 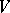 which preserve a fixed flag of type
which preserve a fixed flag of type 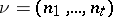 of
of 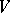 . The quotient space
. The quotient space 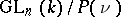 is the variety of all flags of type
is the variety of all flags of type  in the space
in the space 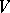 .
.
In the case where 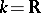 , the parabolic
, the parabolic 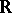 -subgroups admit the following geometric interpretation (see ). Let
-subgroups admit the following geometric interpretation (see ). Let 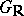 be a non-compact real semi-simple Lie group defined by the group of real points of a semi-simple algebraic group
be a non-compact real semi-simple Lie group defined by the group of real points of a semi-simple algebraic group 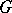 which is defined over
which is defined over 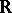 . A subgroup of
. A subgroup of 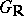 is a parabolic subgroup if and only if it coincides with the group of motions of the corresponding non-compact symmetric space
is a parabolic subgroup if and only if it coincides with the group of motions of the corresponding non-compact symmetric space 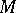 preserving some
preserving some 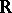 -pencil of geodesic rays of
-pencil of geodesic rays of 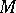 (two geodesic rays of
(two geodesic rays of 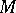 are said to belong to the same
are said to belong to the same 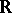 -pencil if the distance between two points, moving with the same fixed velocity along their rays to infinity, has a finite limit).
-pencil if the distance between two points, moving with the same fixed velocity along their rays to infinity, has a finite limit).
A parabolic subgroup of a Tits system 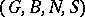 is a subgroup of the group
is a subgroup of the group 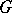 that is conjugate to a subgroup containing
that is conjugate to a subgroup containing 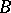 . Each parabolic subgroup coincides with its normalizer. The intersection of any two parabolic subgroups contains a subgroup of
. Each parabolic subgroup coincides with its normalizer. The intersection of any two parabolic subgroups contains a subgroup of  that is conjugate to
that is conjugate to 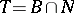 . In particular, a parabolic subgroup of a Tits system associated with a reductive linear algebraic group
. In particular, a parabolic subgroup of a Tits system associated with a reductive linear algebraic group  is the same as a parabolic subgroup of the group
is the same as a parabolic subgroup of the group 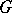 (see [3], [4]).
(see [3], [4]).
References
| [1] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 |
| [2] | A. Borel, J. Tits, "Eléments unipotents et sous-groupes paraboliques de groupes réductifs I" Invent. Math. , 12 (1971) pp. 95–104 |
| [3] | N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII |
| [4] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
| [5] | F.I. Karpelevich, "The geometry of geodesics and the eigenfunctions of the Laplace–Beltrami operator on symmetric spaces" Trans. Moscow Math. Soc. , 14 (1967) pp. 51–199 Trudy Moskov. Mat. Obshch. , 14 (1965) pp. 48–185 |
Comments
References
| [a1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
Parabolic subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_subgroup&oldid=16195