Parabolic coordinates
From Encyclopedia of Mathematics
The numbers  and
and  related to rectangular Cartesian coordinates
related to rectangular Cartesian coordinates  and
and  by the formulas
by the formulas
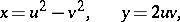 |
where  and
and  . The coordinate lines are two systems of mutually orthogonal parabolas with oppositely-directed axes.
. The coordinate lines are two systems of mutually orthogonal parabolas with oppositely-directed axes.

Figure: p071170a
The Lamé coefficients (or scale factors) are given by:
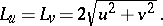 |
The area element is given by:
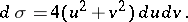 |
The fundamental operators of vector analysis are given by:
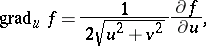 |
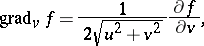 |
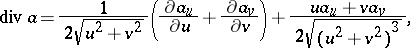 |
 |
In parabolic coordinates the Laplace equation allows separation of variables.
Comments
Using complex functions the coordinate transformation can be described by  , where
, where 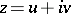 and
and 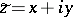 .
.
For parabolic coordinates in space see [a1].
References
| [a1] | R. Sauer (ed.) I. Szabó (ed.) , Mathematische Hilfsmittel des Ingenieurs , 1 , Springer (1967) pp. 98 |
| [a2] | L.D. Landau, E.M. Lifshits, "Mechanics" , Pergamon (1960) pp. 151ff (Translated from Russian) |
How to Cite This Entry:
Parabolic coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_coordinates&oldid=15697
Parabolic coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_coordinates&oldid=15697
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article