Painlevé problem
The problem of characterizing removable sets (cf. Removable set) for a class of bounded single-valued analytic functions of the complex variable  . Let
. Let 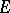 be a compact set in the complex plane
be a compact set in the complex plane 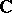 such that
such that 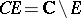 is a domain. One has to determine the minimal conditions on
is a domain. One has to determine the minimal conditions on 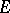 under which any bounded single-valued analytic function in
under which any bounded single-valued analytic function in 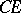 can be continued analytically to
can be continued analytically to 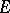 and thus is a constant. P. Painlevé [1] stated a sufficient condition: The linear Hausdorff measure of
and thus is a constant. P. Painlevé [1] stated a sufficient condition: The linear Hausdorff measure of 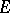 should vanish (such sets are sometimes called Painlevé sets); however, his arguments contain some errors (see [2], [3]). A necessary and sufficient condition on
should vanish (such sets are sometimes called Painlevé sets); however, his arguments contain some errors (see [2], [3]). A necessary and sufficient condition on 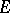 is that the analytic capacity of
is that the analytic capacity of 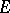 vanishes (Ahlfors' theorem). An example has been constructed of a set with zero analytic capacity but having positive linear measure [5].
vanishes (Ahlfors' theorem). An example has been constructed of a set with zero analytic capacity but having positive linear measure [5].
References
| [1] | P. Painlevé, "Leçons sur la théorie analytique des équations différentielles, professées à Stockholm (1895)" , Paris (1897) |
| [2] | L. Zoretti, "Sur les fonctions analytiques uniformes qui possèdent un ensemble parfait discontinu de points singuliers" J. Math. Pure Appl. , 1 (1905) pp. 1–51 |
| [3] | L. Zoretti, "Leçons sur la prolongement analytique" , Gauthier-Villars (1911) |
| [4] | L. Ahlfors, "Bounded analytic functions" Duke Math. J. , 14 (1947) pp. 1–11 |
| [5] | A.G. Vitushkin, "Example of a set of positive length but of zero analytic capacity" Dokl. Akad. Nauk SSSR , 127 : 2 (1959) pp. 246–249 (In Russian) |
Comments
References
| [a1] | J.B. Garnett, "Analytic capacity and measure" , Lect. notes in math. , 297 , Springer (1972) |
| [a2] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1957) |
| [a3] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Acad. Press (1976) pp. 229ff |
Painlevé problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Painlev%C3%A9_problem&oldid=16072