P-rank
(in group theory)
Let 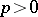 be a prime number. The
be a prime number. The  -rank of a finite group
-rank of a finite group 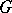 is the largest integer
is the largest integer  such that
such that 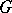 has an elementary Abelian subgroup of order
has an elementary Abelian subgroup of order 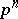 (cf. Abelian group). A
(cf. Abelian group). A  -group is elementary Abelian if it is a direct product of cyclic groups of order
-group is elementary Abelian if it is a direct product of cyclic groups of order 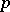 (cf. Cyclic group). A finite group
(cf. Cyclic group). A finite group 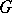 has
has 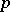 -rank
-rank 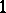 if and only if either the Sylow
if and only if either the Sylow 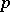 -subgroup (cf. Sylow subgroup) of
-subgroup (cf. Sylow subgroup) of 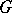 is cyclic or
is cyclic or 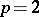 and the Sylow
and the Sylow 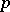 -subgroup of
-subgroup of 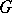 is generalized quarternion. There are several variations on the definition. For example, the normal
is generalized quarternion. There are several variations on the definition. For example, the normal 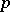 -rank of
-rank of 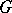 is the maximum of the
is the maximum of the 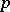 -ranks of the Abelian normal subgroups of
-ranks of the Abelian normal subgroups of 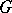 (cf. Normal subgroup). The sectional
(cf. Normal subgroup). The sectional 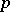 -rank of
-rank of 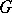 is the maximum of the
is the maximum of the 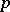 -ranks of the Abelian sections
-ranks of the Abelian sections 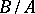 for subgroups
for subgroups 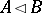 of
of 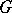 .
.
The notion of 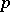 -rank was used extensively to sort out cases in the classification of finite simple groups (cf. Simple finite group). Some details can be found in [a2] and [a3]. In particular, see [a3], Sect. 1.5. In [a2], the word "p-depth of a groupdepth" is used and "rank" is reserved for a different concept. In the cohomology of groups, a celebrated theorem of D. Quillen [a4] states that the
-rank was used extensively to sort out cases in the classification of finite simple groups (cf. Simple finite group). Some details can be found in [a2] and [a3]. In particular, see [a3], Sect. 1.5. In [a2], the word "p-depth of a groupdepth" is used and "rank" is reserved for a different concept. In the cohomology of groups, a celebrated theorem of D. Quillen [a4] states that the 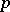 -rank of
-rank of 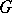 is the same as the Krull dimension (cf. Dimension) of the modulo
is the same as the Krull dimension (cf. Dimension) of the modulo 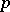 cohomology ring of
cohomology ring of 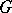 . The connection can be described as follows. Suppose
. The connection can be described as follows. Suppose 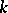 is a field of characteristic
is a field of characteristic 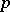 . Let
. Let 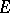 be an elementary Abelian subgroup of order
be an elementary Abelian subgroup of order 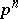 . By direct calculation it can be shown that the cohomology ring of
. By direct calculation it can be shown that the cohomology ring of 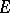 modulo its radical is a polynomial ring in
modulo its radical is a polynomial ring in  variables. Hence its maximal ideal spectrum
variables. Hence its maximal ideal spectrum 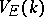 is an affine space of dimension
is an affine space of dimension  . Quillen's theorem says that the restriction mapping
. Quillen's theorem says that the restriction mapping  induces a finite-to-one mapping of varieties
induces a finite-to-one mapping of varieties
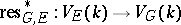 |
and, moreover, 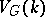 is the union of the images for all
is the union of the images for all 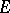 . Therefore, the dimension of
. Therefore, the dimension of 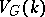 , which is the Krull dimension of
, which is the Krull dimension of 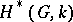 , is the maximum of the
, is the maximum of the 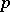 -ranks of the subgroups
-ranks of the subgroups 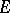 . The theorem has found many applications in modular representation theory (see [a1]).
. The theorem has found many applications in modular representation theory (see [a1]).
References
| [a1] | D. J. Benson, "Representations and cohomology II: cohomology of groups and modules" , Cambridge Univ. Press (1991) |
| [a2] | D. Gorenstein, "Finite groups" , Harper and Row (1968) |
| [a3] | D. Gorenstein, "Finite groups" , Plenum (1982) |
| [a4] | D.G. Quillen, "The spectrum of an equivalent cohomology ring" Ann. of Math. , 94 (1971) pp. 549–602 |
P-rank. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-rank&oldid=13520